
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一个动点(不与
上一个动点(不与![]() 、
、![]() 重合),点
重合),点![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,设
,设![]() .
.
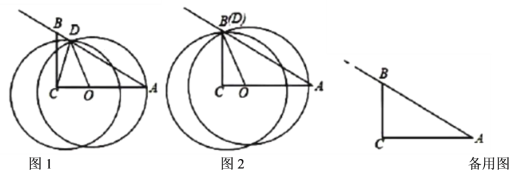
(1)如图2,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)当点![]() 在线段
在线段![]() 上,如果
上,如果![]() 与
与![]() 的另一个交点
的另一个交点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,试求
,试求![]() 与
与![]() 之间的函数解析式,并写出
之间的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)在点![]() 的运动过程中,如果
的运动过程中,如果![]() 与线段
与线段![]() 只有一个公共点,请直接写出
只有一个公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某工厂为全运会设计了一款成本每件20元的工艺品,投放市场试销后发现销售量y(件)是售价x(元/件)的一次函数,当售价为23元/件时,每天销售量为790件;当售价为25元/件,每天销售量为750件.
(1)求y与x的函数关系;
(2)如果该工艺品最高不超过每件30元,那么售价定位每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的半径为
的半径为![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,连接
上一点,连接![]() 、
、![]() .
.![]() 为劣弧
为劣弧![]() 的中点,过点
的中点,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() ,如图2.
,如图2.
①求![]() 的长;
的长;
②图中阴影部分的面积等于_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C将线段AB分成两部分,若AC2=BCAB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(![]() +3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】
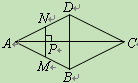

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 的部分图象,其顶点为
的部分图象,其顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,连接
,连接![]() .以下结论:①
.以下结论:①![]() ;②抛物线经过点
;②抛物线经过点![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() .其中正确的是( )
.其中正确的是( )
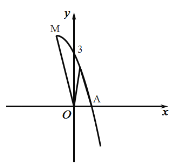
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日,为迎接“世界读书日”,某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会,规则为:一个不透明的袋子中装有4个小球,小球上分别标有数字1,2,3,4,它们除所标数字外完全相同,摇匀后同时从中随机摸出两个小球,则两球所标数字之和与奖励的购书券金额的对应关系如下:
两球所标数字之和 | 3 | 4 | 5 | 6 | 7 |
奖励的购书券金额(元) | 0 | 0 | 30 | 60 | 90 |
(1)通过列表或画树状图的方法计算摸奖一次获得90元购书券的概率;
(2)书城规定:如果顾客不愿意参加摸奖,那么可以直接获得30元的购书券.在“参加摸奖”和“直接获得购书券”两种方式中,你认为哪种方式对顾客更合算?请通过求平均教的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,AB=6,BC=4,点E在边AB上(不与点A、B重合),过点D作DF⊥DE,交边BC的延长线于点F.
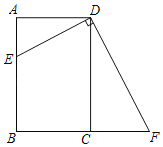
(1)求证:△DAE∽△DCF.
(2)设线段AE的长为x,线段BF的长为y,求y与x之间的函数关系式.
(3)当四边形EBFD为轴对称图形时,则cos∠AED的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com