
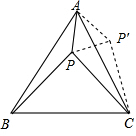
 如图,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=
如图,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,则∠APB= 连结PP′,
连结PP′,

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
A、
| ||||
B、
| ||||
| C、-0.5x3y2与2x2y3是同类项 | ||||
| D、5m2n与-nm2是同类项 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
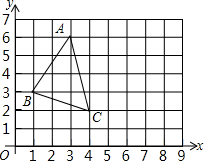 如图,△ABC的顶点坐标分别为A(3,6),B(1,3),C(4,2),将△ABC绕点C顺时针旋转90°,得到△A′B′C.
如图,△ABC的顶点坐标分别为A(3,6),B(1,3),C(4,2),将△ABC绕点C顺时针旋转90°,得到△A′B′C. |
| BB′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
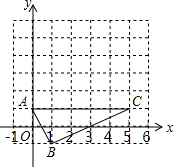 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).查看答案和解析>>
科目:初中数学 来源: 题型:
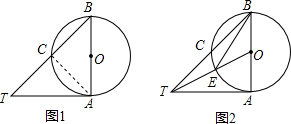 已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.
已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.查看答案和解析>>
科目:初中数学 来源: 题型:
 某公司销售一种市场需求较大的新型产品,每件行星新型产品的进阶为40元,公司要求售价不低于进价,但不高于65元,通过作市场调查,得到数据如图表所示:
某公司销售一种市场需求较大的新型产品,每件行星新型产品的进阶为40元,公司要求售价不低于进价,但不高于65元,通过作市场调查,得到数据如图表所示:| 售格x(元/件) | 50 | 51 | 52 | 53 | … |
| 年销售量y(件) | 500 | 490 | 480 | 470 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com