
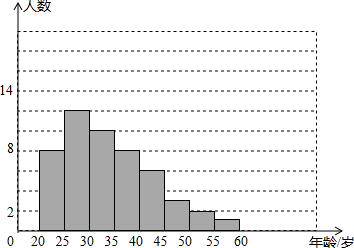
| A、一、二、三象限 |
| B、二、三、四象限 |
| C、一、三、四象限 |
| D、一、二、三、四象限 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
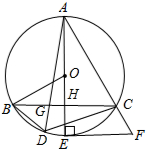 如图,AE为⊙O的直径,EF为⊙O的切线,E为切点,连接AF交⊙O于点C,CB∥EF交AE于H交⊙O于B,D为BC弧上一点,连接AD交BC于G.
如图,AE为⊙O的直径,EF为⊙O的切线,E为切点,连接AF交⊙O于点C,CB∥EF交AE于H交⊙O于B,D为BC弧上一点,连接AD交BC于G.查看答案和解析>>
科目:初中数学 来源: 题型:
 小刚和小强玩飞行棋游戏,想要起飞必须投掷一枚骰子,并且得到6,可以起飞之后同时掷两枚骰子,点数之和即为飞行步数.
小刚和小强玩飞行棋游戏,想要起飞必须投掷一枚骰子,并且得到6,可以起飞之后同时掷两枚骰子,点数之和即为飞行步数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com