
分析 先考虑正负数,再考虑分子和分母的规律:分子依次为1、3、7、13…,第n个数的分子为:n(n-1)+1;分母依次为4、9、16、25、…,第n个数的分母为:(n+1)2;写出第8个数即可.
解答 解:从正负数考虑:第8个数为负数,
不考虑正负,则第1个数为:$\frac{1}{4}$=$\frac{1}{{2}^{2}}$,
第2个数为:$\frac{1}{3}$=$\frac{3}{9}$=$\frac{2×1+1}{{3}^{2}}$,
第3个数为:$\frac{7}{16}$=$\frac{3×2+1}{{4}^{2}}$,
第4个数为:$\frac{13}{25}$=$\frac{4×3+1}{{5}^{2}}$,
…
∴第8个数为:-$\frac{8×7+1}{{8}^{2}}$=-$\frac{57}{64}$,
故答案为:-$\frac{57}{64}$.
点评 本题是数字类的规律题,关键是分子和分母的变化规律,根据给出的数列,归纳、总结出数的变化规律,再由规律解决问题.


科目:初中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,E为边CD上一点,联结AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△ABF:S△DEF=25:4.
如图,在平行四边形ABCD中,E为边CD上一点,联结AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△ABF:S△DEF=25:4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
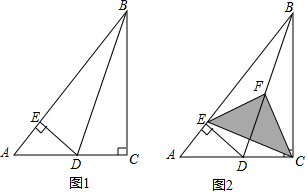 已知△ABC中,∠ACB=90°,∠A=60°,AC=6,点D为AC边上的一个动点,DE⊥AB,垂足为点E.
已知△ABC中,∠ACB=90°,∠A=60°,AC=6,点D为AC边上的一个动点,DE⊥AB,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,点A、E、F、C在同一直线上,且AD=CB,DF=BE,AE=CF,求证:AD∥BC.
如图所示,点A、E、F、C在同一直线上,且AD=CB,DF=BE,AE=CF,求证:AD∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com