
【题目】如图,下列四组条件中,能判定ABCD是正方形的有( )
①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.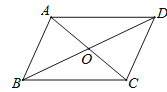
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:①AB=BC,∠A=90°;
根据有一个角是直角且有一组邻边相等的平行四边形是正方形,能判定ABCD是正方形,故此选项正确;
②AC⊥BD,AC=BD;
由对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定ABCD是正方形,故此选项正确;
③OA=OD,BC=CD;
由ABCD是平行四边形,可得AC与BD互相平分,而OA=OD,所以AC=BD,对角线相等的平行四边形是矩形,有一组邻边相等的平行四边形是菱形,既是矩形又是菱形的四边形是正方形,能判定ABCD是正方形,故此选项正确;
④∠BOC=90°,∠ABD=∠DCA;
由∠BOC=90°,根据对角线互相垂直的平行四边形是菱形,可得ABCD是菱形;由ABCD是平行四边形,可得AC与BD互相平分,AB∥CD,则∠ABD=∠CDB=∠DCA,所以OC=OD,又对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定ABCD是正方形,故此选项正确.
故选D.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某蓄水池的横断面示意图如右图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度 ![]() 和放水时间
和放水时间 ![]() 之间的关系的是( )
之间的关系的是( )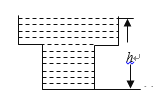
A.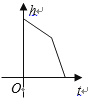
B.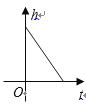
C.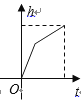
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学所用的路程与时间的关系示意图.根据图中提供的信息回答下列问题: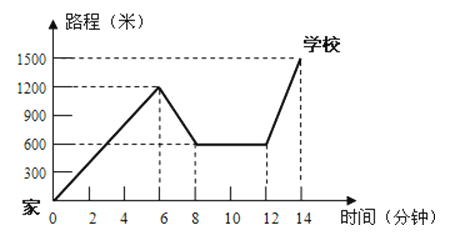
(1)陈杰家到学校的距离是多少米?书店到学校的距离是多少米?
(2)陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?
(3)在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?
(4)如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )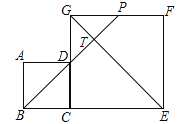
A.2![]()
B.3![]()
C.4![]()
D.6![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com