练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：

    （1）(-3ab)·(-2a)·(-a2b3)；

    （2）(25m2+15m3n-20m4)÷(-5m2)．

    【答案】（1）-6a4b4;（2）-5-3mn+4m2

    【解析】

    （1）根据单项式乘以单项式法则即可解答；（2）根据多项式除以单项式法则即可解答.

    解：（1）(-3ab)·(-2a)·(-a2b3)=-6a4b4;

    （2）(25m2+15m3n-20m4)÷(-5m2)

    =25m2÷（-5m2）+15m3n÷（-5m2）-20m4÷（-5m2）

    =-5-3mn+4m2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，下列四组条件中，能判定ABCD是正方形的有（　　）
    ①AB=BC，∠A=90°；②AC⊥BD，AC=BD；③OA=OD，BC=CD；④∠BOC=90°，∠ABD=∠DCA．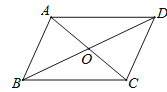

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C＝90°，DE垂直平分AC ， DF⊥BC ， 当△ABC满足条件时，四边形DECF是正方形．（要求：①不再添加任何辅助线，②只需填一个符合要求的条件）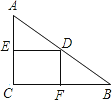

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】雅安地震发生后，全国人民抗震救灾，众志成城，在地震发生一周年之际，某地政府又筹集了重建家园的必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）

    车型

    甲

    乙

    丙

    汽车运载量（吨/辆）

    5

    8

    10

    汽车运费（元/辆）

    400

    500

    600


    （1）全部物资可用甲型车8辆，乙型车5辆，丙型车辆来运送．
    （2）若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？
    （3）为了节省运费，该地政府打算用甲、乙、丙三种车型同时参与运送，已知它们的总辆数为14辆，你能分别求出三种车型的辆数吗？此时的运费又是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，连接BE、DF，DF交对角线AC于点G，且DE=DG．
    （1）求证：AE=CG；
    （2）试判断BE和DF的位置关系，并说明理由．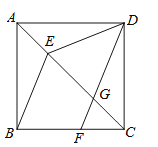

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表，则当y＜5时，x的取值范围是_____．

    x

    …

    ﹣1

    0

    1

    2

    3

    …

    y

    …

    10

    5

    2

    1

    2

    …

    查看答案和解析>>

    科目：初中数学 来源： 题型：

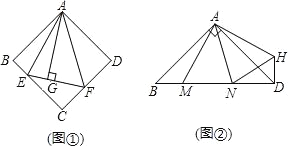
    【题目】（1）如图①，在正方形ABCD中，△AEF的顶点E，F分别在BC，CD边上，高AG与正方形的边长相等，求∠EAF的度数．

    （2）如图②，在Rt△ABD中，∠BAD=90°，AB=AD，点M，N是BD边上的任意两点，且∠MAN=45°，将△ABM绕点A逆时针旋转90°至△ADH位置，连接NH，试判断MN2，ND2，DH2之间的数量关系，并说明理由．

    （3）在图①中，若EG=4，GF=6，求正方形ABCD的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是菱形，对角线AC=16cm，BD=12cm，DH⊥BC于点H，交AC于点G．
    （1）写出两个不全等且与△GHC相似的三角形，并任选其中的一个进行证明；
    （2）求GH的长．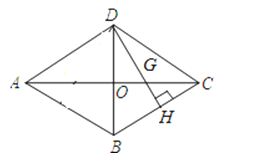

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某日傍晚，黄山的气温由上午的零下2℃下降了7℃，这天傍晚黄山的气温是℃．

    查看答案和解析>>

    同步练习册答案