Question

【题目】如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，连接BE、DF，DF交对角线AC于点G，且DE=DG．
（1）求证：AE=CG；
（2）试判断BE和DF的位置关系，并说明理由．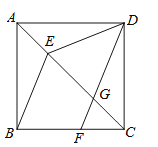

Answer 1

【答案】解：（1）证明：在正方形ABCD中，
∵AD=CD，
∴∠DAE=∠DCG，
∵DE=DG，
∴∠DEG=∠DGE，
∴∠AED=∠CGD．
在△AED和△CGD中，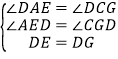

∴△AED≌△CGD（AAS），
∴AE=CG．
（2）解法一：BE∥DF，理由如下：
在正方形ABCD中，AB∥CD，
∴∠BAE=∠DCG．
在△AEB和△CGD中，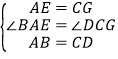

∴△AEB≌△CGD（SAS），
∴∠AEB=∠CGD．
∵∠CGD=∠EGF，
∴∠AEB=∠EGF，
∴BE∥DF．
解法二：BE∥DF，理由如下：
在正方形ABCD中，
∵AD∥FC，
∴=．
∵CG=AE，
∴AG=CE．
又∵在正方形ABCD中，AD=CB，
∴=．
又∵∠GCF=∠ECB，
∴△CGF∽△CEB，
∴∠CGF=∠CEB，
∴BE∥DF．

【解析】（1）先证∠AED=∠CGD，再证明△ADE≌△CDG，根据全等三角形的对应边相等即可得出结论；
（2）先证明△AEB≌△CGD，得出对应角相等∠AEB=∠CGD，得出∠AEB=∠EGF，即可证出平行线．