
【题目】已知:在![]() 中,
中,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]()
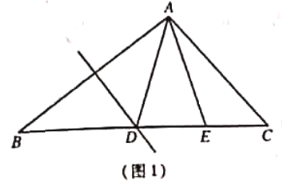
![]() 如图1 ,求证:
如图1 ,求证:![]()
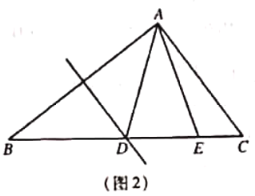
![]() 如图2,当
如图2,当![]() 时.在不添加任何辅助线情况下,请直接写出图2中的四个等腰三角形.
时.在不添加任何辅助线情况下,请直接写出图2中的四个等腰三角形.
【答案】![]() 见解析;
见解析;![]()
![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
![]() 令
令![]() ,根据AB的垂直平分线交BC于点D,求出
,根据AB的垂直平分线交BC于点D,求出![]() , 根据AB=BE求出
, 根据AB=BE求出![]() ,即可得到AD=AE;
,即可得到AD=AE;
(2)根据 AB的垂直平分线交BC于D,得到![]() 是等腰三角形;根据AB=BE,得到△ABE是等腰三角形;由(1)知
是等腰三角形;根据AB=BE,得到△ABE是等腰三角形;由(1)知![]() ,推出△ADE是等腰三角形;求出
,推出△ADE是等腰三角形;求出![]() ,
,![]() ,得到AD=CD,推出△ACD是等腰三角形.
,得到AD=CD,推出△ACD是等腰三角形.
![]() 证明:令
证明:令![]() ,
,
![]() 线段
线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
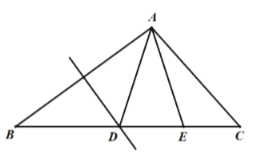
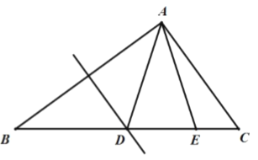
![]() 如图2,
如图2,
∵AB的垂直平分线交BC于D,
∴AD=BD,
∴![]() 是等腰三角形;
是等腰三角形;
∵AB=BE,
∴△ABE是等腰三角形;
由(1)知![]() ,
,
∴△ADE是等腰三角形;
∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴∠DAC=∠C,
∴AD=CD,
∴△ACD是等腰三角形;
∴图中的等腰三角形是:![]() ,
,![]() ,
,![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,直线![]() 交坐标轴于A、C两点,抛物线
交坐标轴于A、C两点,抛物线![]() 过A、C两点.
过A、C两点.
(1)求抛物线的解析式;
(2)若点P为抛物线位于第三象限上一动点,连接PA,PC,试问△PAC是否存在最大值,若存在,请求出△APC取最大值以及点P的坐标,若不存在,请说明理由;
(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里装有两个红球,两个白球和一个蓝球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,两次摸到的球的颜色能配成紫色(红色和蓝色能配成紫色)的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
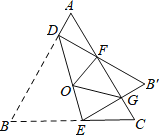
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2![]() ,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
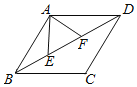
A.4B.4+![]() C.2+2
C.2+2![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视举办的《中国诗词大会》受到广大学生群体广泛关注.某校的诗歌朗诵社团就《中国诗词大会》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中说给信息解答下列问题:
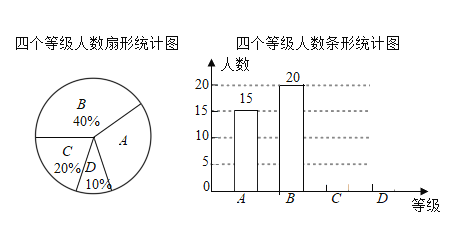
(1)本次被调查对象共有 人,扇形统计图中被调查者“非常喜欢”等级所对应圆心角的度数为 ;
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两名女生,其余是男生,从原“不太喜欢”的人中挑选两名学生了解不太喜欢的原因,请用画树状图或列表法求所选取的这两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养猪场对猪舍进行喷药消毒.在消毒的过程中,先经过![]() 的药物集中喷洒,再封闭猪舍
的药物集中喷洒,再封闭猪舍![]() ,然后再打开窗户进行通风.已知室内每立方米空气中含药量
,然后再打开窗户进行通风.已知室内每立方米空气中含药量![]() (
(![]() )与药物在空气中的持续时间
)与药物在空气中的持续时间![]() (
(![]() )之间的函数图象如图所示,其中在打开窗户通风前
)之间的函数图象如图所示,其中在打开窗户通风前![]() 与
与![]() 分别满足两个一次函数,在通风后
分别满足两个一次函数,在通风后![]() 与
与![]() 满足反比例函数.
满足反比例函数.
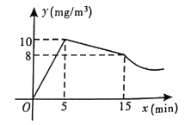
(1)求反比例函数的关系式;
(2)当猪舍内空气中含药量不低于![]() 且持续时间不少于
且持续时间不少于![]() ,才能有效杀死病毒,问此次消毒是否有效?
,才能有效杀死病毒,问此次消毒是否有效?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com