
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.
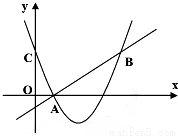
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b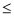 (x-2)2+m的x的取值范围.
(x-2)2+m的x的取值范围.
(1)y=(x-2)2-1,y=x-1;(2)x≤1或x≥4.
【解析】
试题分析:(1)先将点A(1,0)代入y=(x-2)2+m求出m的值,根据点的对称性确定B点坐标,然后根据待定系数法求出一次函数解析式;
(2)根据图象和A、B的交点坐标可直接求出kx+b≤(x-2)2+m的x的取值范围.
试题解析: (1)将点A(1,0)代入y=(x-2)2+m得(1-2)2+m=0,解得m=-1,
所以二次函数解析式为y=(x-2)2-1;
当x=0时,y=4-1=3,
所以C点坐标为(0,3),
由于C和B关于对称轴对称,而抛物线的对称轴为直线x=2,
所以B点坐标为(4,3),
将A(1,0)、B(4,3)代入y=kx+b得
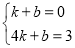 ,解得
,解得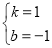 ,
,
所以一次函数解析式为y=x-1;
(2)观察图像可得x的取值范围:x≤1或x≥4.
考点: 1.待定系数法求二次函数解析式;2.待定系数法求一次函数解析式;3.二次函数与不等式(组).


科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
已知关于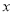 的方程
的方程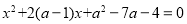 .
.
(1)若方程有两个不相等的实数根,求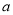 的取值范围;
的取值范围;
(2)若方程的两个实数根为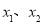 ,且满足
,且满足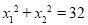 ,求
,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:选择题
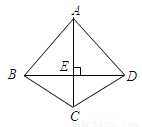
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
A.AB=AD B.AC平分∠BCD C.AB=BD D.△BEC≌△DEC
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州十五中教育集团九年级第二学期3月月考数学试卷(解析版) 题型:选择题
如图,直线y=kx+b经过点A(﹣1,﹣2)和点B(﹣2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )

A.x<﹣2 B.﹣2<x<﹣1 C.﹣2<x<0 D.﹣1<x<0
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州十五中教育集团九年级第二学期3月月考数学试卷(解析版) 题型:选择题
关于近似数2.4×103,下列说法正确的是( )
A.精确到十分位,有2个有效数字 B.精确到百位,有4个有效数字
C.精确到百位,有2个有效数字 D.精确到十分位,有4个有效数字
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:填空题
如图,已知⊙P的半径为2,圆心P在抛物线y= x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为_________.
x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为_________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:选择题
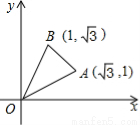
如图,A(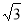 ,1),B(1,
,1),B(1,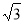 ),将∆AOB绕点O旋转1500后,得到∆A’OB’,则此时点A的对应点A’的坐标为()
),将∆AOB绕点O旋转1500后,得到∆A’OB’,则此时点A的对应点A’的坐标为()
A.(-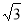 ,1) B.(-2,0)
,1) B.(-2,0)
C.(-1,-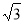 )或(-2,0) D.(-
)或(-2,0) D.(-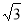 ,-1)或(-2,0)
,-1)或(-2,0)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为 cm2.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:解答题
如图1,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB—BA向点A做匀速运动.
(1)点P将要运行路径AD的长度为 ;点Q将要运行的路径折线CB—BA的长度为 .
(2)当点Q在BA边上运动时,若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式,并求自变量t的取范围;
②求当t为何值时,S有最大值,最大值是多少?
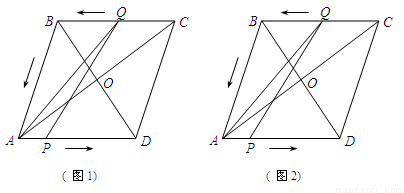
(3)如图2,若点Q的速度为每秒a个单位长(a≤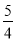 ),当t =4秒时:
),当t =4秒时:
①此时点Q是在边CB上,还是在边BA上呢?
②△APQ是等腰三角形,请求出a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com