
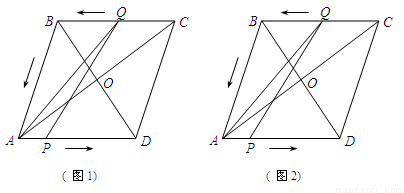
如图1,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB—BA向点A做匀速运动.
(1)点P将要运行路径AD的长度为 ;点Q将要运行的路径折线CB—BA的长度为 .
(2)当点Q在BA边上运动时,若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式,并求自变量t的取范围;
②求当t为何值时,S有最大值,最大值是多少?
(3)如图2,若点Q的速度为每秒a个单位长(a≤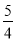 ),当t =4秒时:
),当t =4秒时:
①此时点Q是在边CB上,还是在边BA上呢?
②△APQ是等腰三角形,请求出a的值.
(1)5;10;(2)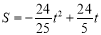 (
(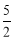 ≤t<5);
≤t<5);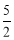 ,6;(3)CB,
,6;(3)CB,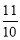 .
.
【解析】
试题分析:(1)根据菱形的性质可知AC⊥BD,且AC与BD互相平分,再根据勾股定理即可求出菱形的边长;
(2)①当0<t≤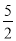 时,由题意,得AP=t,点Q在BC上运动,过点B作BE⊥AD,垂足为E,由直角三角形的性质求出BE的长,由三角形的面积公式可得到S与t的关系式;
时,由题意,得AP=t,点Q在BC上运动,过点B作BE⊥AD,垂足为E,由直角三角形的性质求出BE的长,由三角形的面积公式可得到S与t的关系式;
②当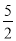 ≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,则QG∥BE,可得出△AQG∽△ABE,由相似三角形的对应边成比例即可得出S关于t的关系式,再根据二次函数的最值问题进行解答即可;
≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,则QG∥BE,可得出△AQG∽△ABE,由相似三角形的对应边成比例即可得出S关于t的关系式,再根据二次函数的最值问题进行解答即可;
(3)先判断出等腰三角形的两腰长,过点Q作QM⊥AP,垂足为点M,QM交AC于点F,根据△AMF∽△AOD∽△CQF,可得出FM的值,由QF=MQ-FM得出QF的值,进而可得出a的值.
试题解析:(1)5;10
(2)当点Q在BA上运动时,5≤2t<10,即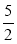 ≤t<5时.
≤t<5时.
如图,过点B作BE⊥AD,垂足为E,过点Q作QG⊥AD,垂足为G,则QG∥BE.

由题意可得BE=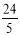 , AP= t,AQ=10-2t.
, AP= t,AQ=10-2t.
∴△AQG∽△ABE, ∴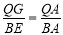 ,
,
∴QG=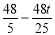 .
.
∴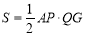 ,
,
即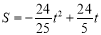 (
(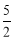 ≤t<5) .
≤t<5) .
∵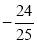 <0,所以s有最大值.
<0,所以s有最大值.
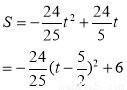
∴当t=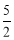 时,S的最大值为6.
时,S的最大值为6.
(3) 【解析】
∵a≤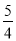 ,则4a≤5,
,则4a≤5,
∴点Q在CB上,
作QM⊥AD于M,QM交AC于点F,则QM为菱形的高.
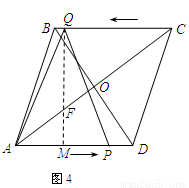
由前面可知,QM=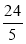 =4.8
=4.8
而当点P运行到点M时,QM最小,
所以PQ≥QM,
∵t=4时,PA=4,∴QM>PA.
∴PQ≥MQ>PA,类似的AQ>MQ>PA
∴QA=QP,△APQ是等腰三角形.
∵QM⊥AP
∴AM=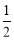 AP=2.由△AMF∽△AOD
AP=2.由△AMF∽△AOD
得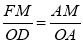 , 而AM=2,OD=3,OA=4
, 而AM=2,OD=3,OA=4
∴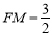 ,
,
∴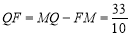 .
.
由△AMF∽△CQF,
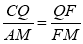 ,而QF=
,而QF=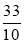 ,FM=
,FM=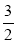 ,AM=2.
,AM=2.
∴CQ= .
.
而当t=4时,CQ=4a
所以4a=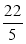 ,解得a=
,解得a=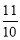 .
.
考点:1.二次函数;2.相似三角形的判定与性质.


科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:解答题
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.
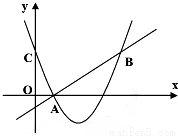
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b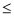 (x-2)2+m的x的取值范围.
(x-2)2+m的x的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:选择题
已知反比例函数y= ,下列结论中不正确的是( )
,下列结论中不正确的是( )
A.图象必经过点(1,﹣5) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则﹣5<y<0
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省邯郸市九年级中考二模数学试卷(解析版) 题型:选择题
如图,在数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数的分别为-5和6,那么,该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省邯郸市九年级中考二模数学试卷(解析版) 题型:选择题
三角形的两边长分别为3和6,第三边的长是方程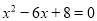 的一个根,则这个三角
的一个根,则这个三角
形的周长是
A.2或4 B.11或13 C.11 D.13
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为
MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为

A.a=b B.2a-b=1 C.2a+b=-1 D.2a+b=1
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:解答题
为进一步规范教育教学行为,切实减轻学生的课业负担,某校想了解本校九年级学生家庭作业用时情况.
(1)确定调查方式时,甲同学说:“我到九年级(1)班去调查全体同学.”乙同学说:“放学时我到校门口随机调查部分同学.”丙同学说:“我到九年级每个班随机调查一定数量的同学.”这三位同学中, 同学的调查方式最合理.
(2)他们采用了最合理的调查方式收集数据,并绘制了如下统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
① ,
, ;
;
②在扇形统计图中,“多于2小时”所对应的扇形的圆心角的度数是 ;
③若该校九年级有900名学生,请你估计有多少学生家庭作业用时不超过1.5小时.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:选择题
一次数学模考后,李老师统计了20名学生的成绩,记录如下:有6人得了85分,有5人得了80分,有4人得了65分,有5人得了90分,则这组数据的中位数和平均数分别是( )
A.82.5,82.5 B.85,81 C.82.5,81 D.85,82.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com