
已知方程 的解是a,求关于y的方程
的解是a,求关于y的方程 的解.
的解.
科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:填空题
如图,已知⊙P的半径为2,圆心P在抛物线y= x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为_________.
x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为_________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省邯郸市九年级中考二模数学试卷(解析版) 题型:解答题
如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.
(1)求证:AC=BD;
(2)若∠AOB=120°,求线段AC,弧CD,线段BD,弧AB组成的封闭图形的面积;
(3)若AB与小圆相切,分别求AB,CD的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省邯郸市九年级中考二模数学试卷(解析版) 题型:选择题
某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为
A. B.
B.
C. D.
D.
 =5
=5
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:解答题
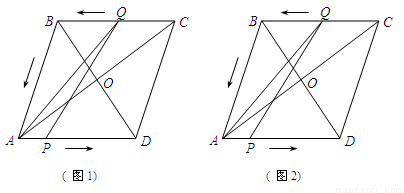
如图1,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB—BA向点A做匀速运动.
(1)点P将要运行路径AD的长度为 ;点Q将要运行的路径折线CB—BA的长度为 .
(2)当点Q在BA边上运动时,若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式,并求自变量t的取范围;
②求当t为何值时,S有最大值,最大值是多少?
(3)如图2,若点Q的速度为每秒a个单位长(a≤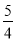 ),当t =4秒时:
),当t =4秒时:
①此时点Q是在边CB上,还是在边BA上呢?
②△APQ是等腰三角形,请求出a的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:选择题
如图,已知抛物线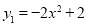 ,直线
,直线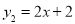 ,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.
,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.

下列给出四个说法:
①当x>0时,y1<y2;
②当x<0时,x值越大,M值越大;
③使得M大于2的x值不存在;
④使得M=1的x值是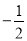 或
或 .
.
说法正确的个数是
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:选择题
某运输公司的一艘轮船在长江上航行,往返于A、B两地.假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从A地出发,逆水航行到B,停留一段时间(卸货、装货、加燃料等),又顺水航行返回A.若该轮船从A出发后所用的时间为x(小时),轮船距A的距离为y(千米),则下列各图形中,能够反映y与x之间函数关系的大致图象是
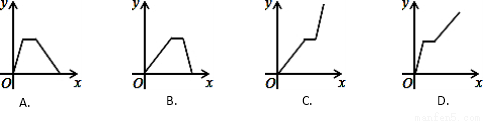
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:解答题
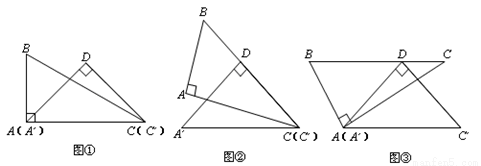
现有一副直角三角板,已知含45°角的直角三角板的斜边恰与含30°角的直角三角板的较长直角边完全重合(如图①).即△C?DA?的顶点A?、C?分别与△BAC的顶点A、C重合.现在让△C?DA?固定不动,将△BAC通过变换使斜边BC经过△C?DA?的直角顶点D.
(1)如图②,将△BAC绕点C按顺时针方向旋转角度α(0°<α<180°),使BC边经过点D,则α= °
(2)如图③,将△BAC绕点A按逆时针方向旋转,使BC边经过点D.试说明:BC∥A?C?.
(3)如图④,若将△BAC沿射线A?C?方向平移m个单位长度,使BC边经过点D,已知AB= ,求m的值.
,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com