
【题目】已知A、B两个村庄的坐标分别为(2,2),(7,4),一辆汽车(看成点P)在![]() 轴上行驶.试确定下列情况下汽车(点P)的位置:
轴上行驶.试确定下列情况下汽车(点P)的位置:
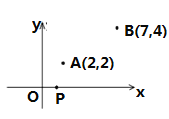
(1)求直线AB的解析式,且确定汽车行驶到什么点时到A、B两村距离之差最大?
(2)汽车行驶到什么点时,到A、B两村距离相等?
【答案】(1)当汽车行使到(3,0)时,到A、B两村距离之差最大.(2)所求点的坐标是(5.7,0).
【解析】
(1)利用待定系数法即可求得直线AB的解析式,当汽车行驶到直线AB上时,到A,B两村的距离之差最大,即可求得点的坐标;
(2)本题即为求线段AB的中垂线与x轴的交点.根据两点之间的距离公式即可求解.
(1)设直线AB的解析式是y=kx+b.
根据题意得![]() ,解得:
,解得:![]() ,
,
则直线AB的解析式是y=![]() .
.
在解析式中,令y=0,解得:x=3.
即当汽车行使到(3,0)时,到A、B两村距离之差最大.
(2)设汽车行驶到(x,0)点时,到A、B两村距离相等.
根据题意得:(7x)2+16=(x2)2+4.
解得:x=5.7,
故所求点的坐标是(5.7,0).


科目:初中数学 来源: 题型:
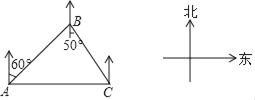
【题目】如图,淇淇一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,C地恰好位于A地正东方向上,则( )
①B地在C地的北偏西50°方向上;
②A地在B地的北偏西30°方向上;
③cos∠BAC=![]() ;
;
④∠ACB=50°.其中错误的是( )
A. ①② B. ②④ C. ①③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,![]() ,点
,点![]() .
.
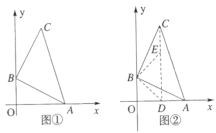
(1)在图①中,点![]() 坐标为__________;
坐标为__________;
(2)如图②,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,作等腰直角三角形
,作等腰直角三角形![]() ,
,![]() ,连接
,连接![]() .证明:
.证明:![]() ;
;
(3)在图②的条件下,若![]() 三点共线,求
三点共线,求![]() 的长;
的长;
(4)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 面积为2.请直接写出所有满足条件的点
面积为2.请直接写出所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,
作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A.11+![]() B.11-
B.11-![]()
C.11+![]() 或11-
或11-![]() D.11-
D.11-![]() 或1+
或1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
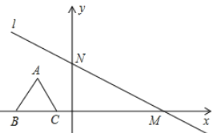
【题目】如图,在平面直角坐标系中,有一条直线l:y=![]() +4与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移
+4与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移
(1)在平移过程中,得到△A1B1C1,此时顶点A1恰落在直线l上,写出A1点的坐标;
(2)继续向右平移,得到△A2B2C2,此时△A2B2C2的三边中垂线的交点P(即外心)恰好落在直线l上,求P点的坐标;
(3)在直线l上是否存在这样的点,与(2)中的A2、B2、C2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=8cm,水面最深地方的高度为2cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=12cm2,则阴影部分面积S=( )cm2.
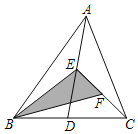
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.则下列结论正确的有( )
S△FGH;④AG+DF=FG.则下列结论正确的有( )
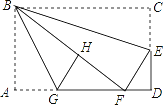
A. ①②④ B. ①③④ C. ②③④ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com