
【题目】已知抛物线y=﹣x2+bx+c过点A(﹣1,0),B(3,0).
(1)求b,c的值;
(2)请用列表、描点、连线的方法画出该函数的图象;
(3)当﹣2<x<2时,y的取值范围是 .
(4)若(m,y1),(m﹣1,y2)是抛物线上的两点,比较y1与y2大小.
【答案】(1)b=2,c=3;(2)详见解析;(3) ﹣5<y≤4;(4)详见解析.
【解析】
(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c中即可求得b、c的值;(2)用列表、描点、连线的方法在所给的坐标系中画出抛物线的图像即可;(3)先求得抛物线的对称轴,结合图象即可解答;(4)由(m,y1),(m﹣1,y2)是抛物线上的两点,可得y1=﹣m2+2m+3,y2=﹣(m﹣1)2+2(m﹣1)+3,利用作差法比较即可.
解:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c中,
得:![]() ,
,
解得:![]() .
.
则抛物线解析式为y=﹣x2+2x+3;
(2)列表
x | ﹣1 | 0 | 1 | 2 | 3 |
y | 0 | 3 | 4 | 3 | 0 |
描点、连线作图如下:
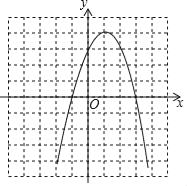
(3)由(1)可知抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,即抛物线对称轴为x=1,
所以当x=1时,y最大=4;当x=﹣2时,y最小=﹣5;
故当﹣2<x<2时,y的范围为﹣5<y≤4;
(4)∵(m,y1),(m﹣1,y2)是抛物线上的两点,
∴y1=﹣m2+2m+3,y2=﹣(m﹣1)2+2(m﹣1)+3,
∵y1﹣y2=﹣m2+2m+3﹣[﹣(m﹣1)2+2(m﹣1)+3]=﹣2m+3,
当﹣2m+3>0,即m<![]() 时,y1>y2;
时,y1>y2;
当﹣2m+3<0,即m>![]() 时,y1<y2;
时,y1<y2;
当﹣2m+3=0,即m=![]() 时,y1=y2.
时,y1=y2.


科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条笔直的公路上有甲、乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发,运动的时间为![]() (分),与乙地的距离为
(分),与乙地的距离为![]() (米),图中线段EF,折线
(米),图中线段EF,折线![]() 分别表示两人与乙地距离
分别表示两人与乙地距离![]() 和运动时间
和运动时间![]() 之间的函数关系图象
之间的函数关系图象
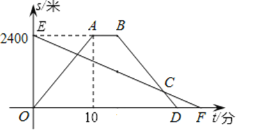
(1)李越骑车的速度为 米/分钟;F点的坐标为 ;
(2)求李越从乙地骑往甲地时, ![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)求王明从甲地到乙地时, ![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(4)求李越与王明第二次相遇时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
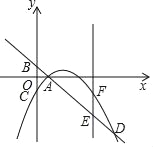
【题目】如图,在平面直角坐标系中,直线y=﹣x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx﹣2与y轴交点C,与直线AB的另一个交点为D,点E是线段AD上一点,点F在抛物线上,EF∥y轴,设E的横坐标为m
(1)用含a的代数式表示b.
(2)当点D的横坐标为8时,求出a的值.
(3)在(2)的条件下,设△ABF的面积为S,求出S最大值,并求出此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传承经典,某市开展“中华古诗词”朗读大赛,某中学甲、乙两名选手经过八轮预赛后脱颖而出,甲、乙两名学生的成绩如图所示,甲、乙两名学生成绩的相关统计数据如表所示,请结合图表回答下列问题:

平均数 | 方差 | |
甲 |
| 118.25 |
乙 | 80 |
|
(1)甲、乙两名同学预赛成绩的中位数分别是:甲__________分,乙___________分;
(2)王老师说,两个人的平均水平相当,不知道选谁参加决赛,但李老师说,乙同学的成绩稳定,请你先计算出![]() 的值并选择所学过的平均数、方差等统计知识,对两位老师的观点进行解释;
的值并选择所学过的平均数、方差等统计知识,对两位老师的观点进行解释;
(3)若学校想从两名选手中选择一名冲击决赛金牌,会选择谁参加?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了防止水土流失,某村开展绿化荒山活动,计划经过若干年使本村绿化总面积新增360万平方米.自2014年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.问实际每年绿化面积多少万平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com