
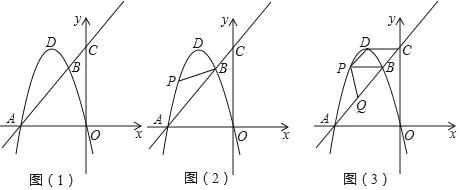
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2﹣2ax与x轴相交于O、A两点,OA=4,点D为抛物线的顶点,并且直线y=kx+b与该抛物线相交于A、B两点,与y轴相交于点C,B点的横坐标是﹣1.
(1)求k,a,b的值;
(2)若P是直线AB上方抛物线上的一点,设P点的横坐标是t,△PAB的面积是S,求S关于t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,当PB∥CD时,点Q是直线AB上一点,若∠BPQ+∠CBO=180°,求Q点坐标.
【答案】(1)k=1、a=2、b=4;(2)s=﹣![]() t2﹣
t2﹣![]() t﹣6,自变量t的取值范围是﹣4<t<﹣1;(3)Q(﹣
t﹣6,自变量t的取值范围是﹣4<t<﹣1;(3)Q(﹣![]() ,
,![]() )
)
【解析】
(1)根据题意可得A(-4,0)代入抛物线解析式可得a,求出抛物线解析式,根据B的横坐标可求B点坐标,把A,B坐标代入直线解析式,可求k,b
(2)过P点作PN⊥OA于N,交AB于M,过B点作BH⊥PN,设出P点坐标,可求出N点坐标,即可以用t表示S.
(3)由PB∥CD,可求P点坐标,连接OP,交AC于点R,过P点作PN⊥OA于M,交AB于N,过D点作DT⊥OA于T,根据P的坐标,可得∠POA=45°,由OA=OC可得∠CAO=45°则PO⊥AB,根据抛物线的对称性可知R在对称轴上.设Q点坐标,根据△BOR∽△PQS,可求Q点坐标.
(1)∵OA=4
∴A(﹣4,0)
∴﹣16+8a=0
∴a=2,
∴y=﹣x2﹣4x,当x=﹣1时,y=﹣1+4=3,
∴B(﹣1,3),
将A(﹣4,0)B(﹣1,3)代入函数解析式,得![]() ,
,
解得![]() ,
,
直线AB的解析式为y=x+4,
∴k=1、a=2、b=4;
(2)过P点作PN⊥OA于N,交AB于M,过B点作BH⊥PN,如图1,
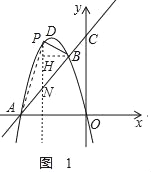
由(1)知直线AB是y=x+4,抛物线是y=﹣x2﹣4x,
∴当x=t时,yP=﹣t2﹣4t,yN=t+4
PN=﹣t2﹣4t﹣(t+4)=﹣t2﹣5t﹣4,
BH=﹣1﹣t,AM=t﹣(﹣4)=t+4,
S△PAB=![]() PN(AM+BH)=
PN(AM+BH)=![]() (﹣t2﹣5t﹣4)(﹣1﹣t+t+4)=
(﹣t2﹣5t﹣4)(﹣1﹣t+t+4)=![]() (﹣t2﹣5t﹣4)×3,
(﹣t2﹣5t﹣4)×3,
化简,得s=﹣![]() t2﹣
t2﹣![]() t﹣6,自变量t的取值范围是﹣4<t<﹣1;
t﹣6,自变量t的取值范围是﹣4<t<﹣1;
∴﹣4<t<﹣1
(3)y=﹣x2﹣4x,当x=﹣2时,y=4即D(﹣2,4),当x=0时,y=x+4=4,即C(0,4),
∴CD∥OA
∵B(﹣1,3).
当y=3时,x=﹣3,
∴P(﹣3,3),
连接OP,交AC于点R,过P点作PN⊥OA于M,交AB于N,过D点作DT⊥OA于T,如图2,
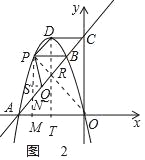
可证R在DT上
∴PN=ON=3
∴∠PON=∠OPN=45°
∴∠BPR=∠PON=45°,
∵OA=OC,∠AOC=90°
∴∠PBR=∠BAO=45°,
∴PO⊥AC
∵∠BPQ+∠CBO=180,
∴∠BPQ=∠BCO+∠BOC
过点Q作QS⊥PN,垂足是S,
∴∠SPQ=∠BOR∴tan∠SPQ=tan∠BOR,
可求BR=![]() ,OR=2
,OR=2![]() ,
,
设Q点的横坐标是m,
当x=m时y=m+4,
∴SQ=m+3,PS=﹣m﹣1
∴![]() ,解得m=﹣
,解得m=﹣![]() .
.
当x=﹣![]() 时,y=
时,y=![]() ,
,
Q(﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)请求出抛物线的解析式;
(2)当0<x<4时,请直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
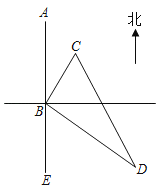
【题目】如图所示,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区D位于B的南偏东55°方向,无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到D需飞行15分钟.若无人机的配送路线是B→C→D→B请求出配送途中飞行所需时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地一路段修建,甲队单独完成这项工程需要60天,若由甲队先做5天,再由甲、乙两队合作9天,共完成这项工程的三分之一.
(1)求甲、乙两队合作完成这项工程需要多少天?
(2)若甲队的工作效率提高20%,乙队工作效率提高50%,甲队施工1天需付工程款4万元,乙队施工一天需付工程款2.5万元,现由甲乙两队合作若干天后,再由乙队完成剩余部分,在完成此项工程的工程款不超过190万元的条件下要求尽早完成此项工程,则甲、乙两队至多要合作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于
,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于![]() 的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
①AD是![]() 的平分线;②
的平分线;②![]() ;③点D在AB的中垂线上;④
;③点D在AB的中垂线上;④![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AB=3,E在AC上且AE=![]() AC,D是直线BC上一动点,线段ED绕点E逆时针旋转900,得到线段EF,当点D运动时,则线段AF的最小值是_______
AC,D是直线BC上一动点,线段ED绕点E逆时针旋转900,得到线段EF,当点D运动时,则线段AF的最小值是_______
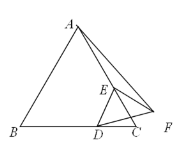
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
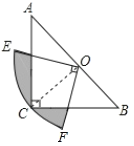
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com