
ЁОЬтФПЁПФГЕивЛТЗЖЮаоНЈЃЌМзЖгЕЅЖРЭъГЩетЯюЙЄГЬашвЊ60ЬьЃЌШєгЩМзЖгЯШзі5ЬьЃЌдйгЩМзЁЂввСНЖгКЯзї9ЬьЃЌЙВЭъГЩетЯюЙЄГЬЕФШ§ЗжжЎвЛЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНЖгКЯзїЭъГЩетЯюЙЄГЬашвЊЖрЩйЬьЃП
ЃЈ2ЃЉШєМзЖгЕФЙЄзїаЇТЪЬсИп20%ЃЌввЖгЙЄзїаЇТЪЬсИп50%ЃЌМзЖгЪЉЙЄ1ЬьашИЖЙЄГЬПю4ЭђдЊЃЌввЖгЪЉЙЄвЛЬьашИЖЙЄГЬПю2.5ЭђдЊЃЌЯжгЩМзввСНЖгКЯзїШєИЩЬьКѓЃЌдйгЩввЖгЭъГЩЪЃгрВПЗжЃЌдкЭъГЩДЫЯюЙЄГЬЕФЙЄГЬПюВЛГЌЙ§190ЭђдЊЕФЬѕМўЯТвЊЧѓОЁдчЭъГЩДЫЯюЙЄГЬЃЌдђМзЁЂввСНЖгжСЖрвЊКЯзїЖрЩйЬьЃП
ЁОД№АИЁПЃЈ1ЃЉМзЁЂввСНЖгКЯзїЭъГЩетЯюЙЄГЬашвЊ36ЬьЃЛЃЈ2ЃЉМзЁЂввСНЖгжСЖрвЊКЯзї7Ьь
ЁОНтЮіЁП
ЃЈ1ЃЉЩшМзЁЂввСНЖгКЯзїЭъГЩетЯюЙЄГЬашвЊxЬьЃЌИљОнЬѕМўЃКМзЖгЯШзі5ЬьЃЌдйгЩМзЁЂввКЯзї9ЬьЃЌЙВЭъГЩзмЙЄзїСПЕФ![]() ЃЌСаЗНГЬЧѓНтМДПЩЃЛ
ЃЌСаЗНГЬЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЩшМзЁЂввСНЖгзюЖрКЯзїдЊЬьЃЌЯШЧѓГіМзЁЂввСНЖгКЯзївЛЬьЭъГЩЙЄГЬЕФЖрЩйЃЌдйИљОнЭъГЩДЫЯюЙЄГЬЕФЙЄГЬПюВЛГЌЙ§190ЭђдЊЃЌСаГіВЛЕШЪНЃЌЧѓНтМДПЩЕУГіД№АИЃЎ
ЃЈ1ЃЉЩшМзЁЂввСНЖгКЯзїЭъГЩетЯюЙЄГЬашвЊxЬь
ИљОнЬтвтЕУЃЌ![]() ЃЌ
ЃЌ
НтЕУ x=36ЃЌ
ОМьбщx=36ЪЧЗжЪНЗНГЬЕФНтЃЌ
Д№ЃКМзЁЂввСНЖгКЯзїЭъГЩетЯюЙЄГЬашвЊ36ЬьЃЌ
ЃЈ2ЃЉ![]()
ЩшМзЁЂввашвЊКЯзїyЬьЃЌИљОнЬтвтЕУЃЌ
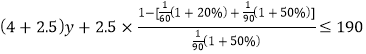 ЃЌ
ЃЌ
НтЕУyЁм7
Д№ЃКМзЁЂввСНЖгжСЖрвЊКЯзї7ЬьЃЎ


 ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛеХШ§НЧаЮжНЦЌ![]() ШчЭММз
ШчЭММз![]() ЃЌЦфжа
ЃЌЦфжа![]() НЋжНЦЌбиЙ§ЕуBЕФжБЯпелЕўЃЌЪЙЕуCТфЕНABБпЩЯЕФEЕуДІЃЌелКлЮЊ
НЋжНЦЌбиЙ§ЕуBЕФжБЯпелЕўЃЌЪЙЕуCТфЕНABБпЩЯЕФEЕуДІЃЌелКлЮЊ![]() ШчЭМвв
ШчЭМвв![]() дйНЋжНЦЌбиЙ§ЕуEЕФжБЯпелЕўЃЌЕуAЧЁКУгыЕуDжиКЯЃЌелКлЮЊ
дйНЋжНЦЌбиЙ§ЕуEЕФжБЯпелЕўЃЌЕуAЧЁКУгыЕуDжиКЯЃЌелКлЮЊ![]() ШчЭМБћ
ШчЭМБћ![]() дШ§НЧаЮжНЦЌABCжаЃЌ
дШ§НЧаЮжНЦЌABCжаЃЌ![]() ЕФДѓаЁЮЊ______
ЕФДѓаЁЮЊ______![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
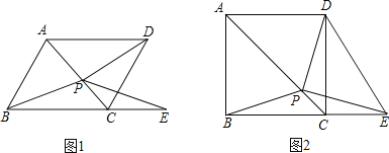
ЁОЬтФПЁП ШчЭМ1ЃЌPЪЧСтаЮABCDЖдНЧЯпACЩЯЕФвЛЕуЃЌЕуEдкBCЕФбгГЄЯпЩЯЃЌЧвPE=PBЃЎ
ЃЈ1ЃЉЧѓжЄЃКPD=PEЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁЯDPE=ЁЯABCЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБЫФБпаЮABCDЮЊе§ЗНаЮЪБЃЌСЌНгDEЃЌЪдЬНОПЯпЖЮDEгыЯпЖЮBPЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП дФЖСЯТУцЕФВФСЯЃЌНтД№КѓУцЕФЮЪЬт
ВФСЯЃКЁАНтЗНГЬx4-3x2+2=0ЁБЁБ
НтЃКЩшx2=yЃЌдЗНГЬБфЮЊy2-3y+2=0ЃЌЃЈy-1ЃЉЃЈy-2ЃЉ=0ЃЌЕУy=1Лђy=2
ЕБy=1ЪБЃЌМДx2=1ЃЌНтЕУx=ЁР1ЃЛ
ЕБy=2ЪБЃЌМДx2=2ЃЌНтЕУx=ЁР![]()
злЩЯЫљЪіЃЌдЗНГЬЕФНтЮЊx1=1ЃЌx2=-1ЃЌx3=![]() ЃЎx4=-
ЃЎx4=-![]()
ЮЪЬтЃКЃЈ1ЃЉЩЯЪіНтД№Й§ГЬВЩгУЕФЪ§бЇЫМЯыЗНЗЈЪЧ______
AЃЎМгМѕЯћдЊЗЈ BЃЎДњШыЯћдЊЗЈ CЃЎЛЛдЊЗЈ DЃЎД§ЖЈЯЕЪ§ЗЈ
ЃЈ2ЃЉВЩгУРрЫЦЕФЗНЗЈНтЗНГЬЃКЃЈx2-2xЃЉ2-x2+2x-6=0ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
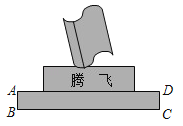
ЁОЬтФПЁПШчЭМЪЧФГжабЇаЃдАФкаТНЈЕФвЛзљЬкЗЩЕёЫмЃЌЪ§бЇРЯЪІИјАЫФъМЖЕФСНИіЪ§бЇЩчЭХВМжУСЫбщжЄЕёЫмЕззље§УцЕФБпABКЭБпCDЪЧЗёЗжБ№ДЙжБгкЕзБпBCЕФзївЕЃЎРЯЪІИјЧЩЪжЩчЭХХфБИЕФЙЄОпжЛгаОэГпЃЌИјУєЫМЩчЭХжЛХфБИСЫвЛАб20cmГЄЕФПЬЖШГпЫћУЧФмЭъГЩШЮЮёТ№ЃПШчЙћФмЃЌЧыИјГіВтСПЗНАИЃЛШчЙћВЛФмашвЊдіМгФФаЉВтСПЙЄОпЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
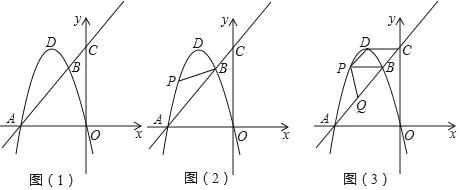
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=Љx2Љ2axгыxжсЯрНЛгкOЁЂAСНЕуЃЌOA=4ЃЌЕуDЮЊХзЮяЯпЕФЖЅЕуЃЌВЂЧвжБЯпy=kx+bгыИУХзЮяЯпЯрНЛгкAЁЂBСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌBЕуЕФКсзјБъЪЧЉ1ЃЎ
ЃЈ1ЃЉЧѓkЃЌaЃЌbЕФжЕЃЛ
ЃЈ2ЃЉШєPЪЧжБЯпABЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌЩшPЕуЕФКсзјБъЪЧtЃЌЁїPABЕФУцЛ§ЪЧSЃЌЧѓSЙигкtЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБPBЁЮCDЪБЃЌЕуQЪЧжБЯпABЩЯвЛЕуЃЌШєЁЯBPQ+ЁЯCBO=180ЁуЃЌЧѓQЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГШЫЮЊСЫВтСПаЁЩНЖЅЩЯЕФЫўEDЕФИпЃЌЫћдкЩНЯТЕФЕуAДІВтЕУЫўМтЕуDЕФбіНЧЮЊ45ЁуЃЌдйбиACЗНЯђЧАНј60 mЕНДяЩННХЕуBЃЌВтЕУЫўМтЕуDЕФбіНЧЮЊ60ЁуЃЌЫўЕзЕуEЕФбіНЧЮЊ30ЁуЃЌЧѓЫўEDЕФИпЖШЃЎ(НсЙћБЃСєИљКХ)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
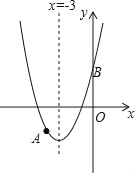
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=x2+bx+cЙ§ЕуAЃЈЉ4ЃЌЉ3ЃЉЃЌгыyжсНЛгкЕуBЃЌЖдГЦжсЪЧx=Љ3ЃЌЧыНтД№ЯТСаЮЪЬтЃК
(1)ЧѓХзЮяЯпЕФНтЮіЪН.
(2)ШєКЭxжсЦНааЕФжБЯпгыХзЮяЯпНЛгкCЃЌDСНЕуЃЌЕуCдкЖдГЦжсзѓВрЃЌЧвCD=8ЃЌЧѓЁїBCDЕФУцЛ§.зЂЃКХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЪЧx=Љ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪГЦЗСуЪлЕъЮЊЪГЦЗГЇДњЯњвЛжжУцАќЃЌЮДЪлГіЕФУцАќПЩвдЭЫЛиГЇМвЃЎОЭГМЦЯњЪлЧщПіЗЂЯжЃЌЕБетжжУцАќЕФЯњЪлЕЅМлЮЊ7НЧЪБЃЌУПЬьТєГі160ИіЃЎдкДЫЛљДЁЩЯЃЎЕЅМлУПЬсИп1НЧЪБЃЌИУСуЪлЕъУПЬьОЭЛсЩйТєГі20ИіУцАќЃЎЩшетжжУцАќЕФЯњЪлЕЅМлЮЊxНЧ(УПИіУцАќЕФГЩБОЪЧ5НЧ)ЃЎСуЪлЕъУПЬьЯњЪлетжжУцАќЕФРћШѓЮЊyНЧЃЎ
(1)гУКЌxЕФДњЪ§ЪНЗжБ№БэЪОГіУПИіУцАќЕФРћШѓгыТєГіЕФУцАќИіЪ§ЃЛ
(2)ЧѓxгыyжЎМфЕФКЏЪ§ЙиЯЕЪНЃК
(3)ЕБетжжУцАќЕФЯњЪлЕЅМлЖЈЮЊЖрЩйЪБЃЌИУСуЪлЕъУПЬьЯњЪлетжжУцАќЛёЕУЕФРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com