
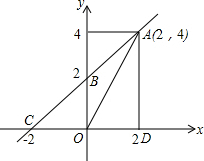
 如图一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,求直线AB的一次函数解析式及△AOC的面积.
如图一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,求直线AB的一次函数解析式及△AOC的面积. 分析 (1)根据待定系数法即可求得;
(2)根据三角形面积公式即可求得.
解答 解:∵一次函数y=kx+b经过点A(2,4)和B(0,2)两点;
∴$\left\{{\begin{array}{l}{4=2k+b}\\{2=b}\end{array}}\right.$
∴$\left\{{\begin{array}{l}{k=1}\\{b=2}\end{array}}\right.$
∴所求一次函数为y=x+2,
∵点C(-2,0)
∴OC=2;
∴${S_{△AOC}}=\frac{1}{2}•OC•|{y_A}|=\frac{1}{2}×2×4=4$.
点评 本题考查了待定系数法求一次函数的解析式,三角形的面积,熟练掌握待定系数法是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.5cm | B. | 2cm | C. | 3cm | D. | 4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
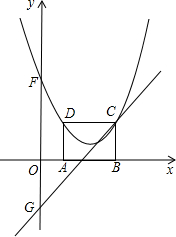 如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2,直线y=x-2经过点C,交y轴于点G.
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2,直线y=x-2经过点C,交y轴于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d(x) | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解巫溪网“今日巫溪”栏目的阅览率 | |
| B. | 了解某甲型H1N1确诊病人同机乘客的健康状况 | |
| C. | 了解某班每个学生家庭电脑的数量 | |
| D. | 对“歼20”隐形战斗机零部件的检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2)2=1 | B. | (x+2)2=5 | C. | (x+2)2=9 | D. | (x+4)2=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com