
����Ŀ����ֱ�����ǰ�ABC����ͼ1���ã�ֱ�Ƕ���C������ԭ���غϣ�ֱ�DZ�AC��BC�ֱ���x���y���غϣ����С�ABC��30�����������ǰ���y������ƽ�ƣ�����Bƽ�Ƶ�ԭ��Oʱ�˶�ֹͣ����ƽ�Ƶľ���Ϊm��ƽ�ƹ��������ǰ����ڵ�һ�����ֵ����Ϊs��s����m�ĺ���ͼ����ͼ2��ʾ����m���ཻ�ڵ�P��![]() ��0������s���ཻ�ڵ�Q��
��0������s���ཻ�ڵ�Q��
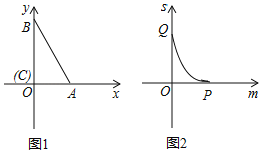
��1����ȷ�����ǰ�ABC�������
��2����ƽ��ǰAB������ֱ�ߵĽ���ʽ��
��3����s����m�ĺ�����ϵʽ����д��Q������꣮
���𰸡���1��S��![]() ����2��y����
����2��y����![]() x+
x+![]() ����3��s��
����3��s��![]() ��m+
��m+![]() ����0��m��
����0��m��![]() ����Q��0��
����Q��0��![]() ����
����
��������
��1�����ݵ�P����ɵ�OB�ij������ݺ�30���ǵ�ֱ�������ε����ʼ����ɶ��������OA�ij������������ABC�������
��2����AB�Ľ���ʽy��kx+b����A��1��0����B��0��![]() �������з����鼴�����b��k��ֵ�������ɵ�ֱ��AB����ʽ��
�������з����鼴�����b��k��ֵ�������ɵ�ֱ��AB����ʽ��
��3�����ƶ������У�AB��x��Ľ���ΪD���ɵ�OB=![]() -m�����ݺ�30���ǵ�ֱ�������ε����ʿ���m��ʾ��OD�ij������ɵó�s����m�Ĺ�ϵʽ����m=0���뼴�������Q���꣮
-m�����ݺ�30���ǵ�ֱ�������ε����ʿ���m��ʾ��OD�ij������ɵó�s����m�Ĺ�ϵʽ����m=0���뼴�������Q���꣮
����m���ཻ�ڵ�P��![]() ��0����
��0����
��m=![]() ʱ��s=0��
ʱ��s=0��
��OB��![]() ��
��
�ߡ�ABC��30����
��AB=2OA��
��OA2+OB2=AB2����OA2+3=4OA2��
��ã�OA=1������ֵ��ȥ��
��S��ABC��![]() ��
��![]() ��
��
��2����B��0��![]() ����A��1��0����
����A��1��0����
��AB�Ľ���ʽy��kx+b��
��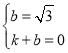 ��
��
�� ��
��
��y����![]() x+
x+![]() ��
��
��3�����ƶ������У�AB��x��Ľ���ΪD��
��OB=![]() ��ƽ�Ƶľ���Ϊm��
��ƽ�Ƶľ���Ϊm��
��ƽ�ƺ�OB��![]() ��m��
��m��
�ߡ�ABC=30����
��BD=2OD��
��OD2+OB2=BD2����OD2+��![]() ��m��2=4OD2
��m��2=4OD2
��OD��1��![]() m��
m��
��s�ڵ�һ���ޣ�OB=![]() ��
��
��0��m��![]() ��
��
��s��![]() ����
����![]() ��m������1��
��m������1��![]() m����
m����![]() ��m+
��m+![]() ��0��m��
��0��m��![]() ����
����
��m��0ʱ��s��![]() ��
��
��Q��0��![]() ����
����
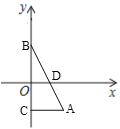


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¶���һ��������:����ƽ���͵��ڵ�����ƽ����4���������ν�����̬����������:ij���������߳��ֱ���5��6��8����Ϊ![]() ����������������dz�̬������.
����������������dz�̬������.
(1)����ABC���߳��ֱ���2��![]() ��4����������� ��̬������(������������������);
��4����������� ��̬������(������������������);
(2)��ͼ��Rt��ABC�У���ACB=90����BC=6����DΪAB���е㣬����CD��CD=![]() AB�� ����ACD�dz�̬�����Σ����ABC�����;��
AB�� ����ACD�dz�̬�����Σ����ABC�����;��
(3)��Rt��ABC�dz�̬����б����![]() ����������ε���ֱ�DZߵĺ�= .
����������ε���ֱ�DZߵĺ�= .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
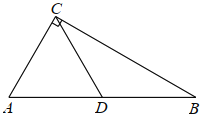
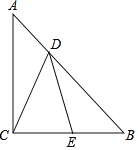
����Ŀ����ͼ����ABC�У�AC��BC����ACB��90������D��AB�ϣ���E��BC�ϣ���AD��BE��BD��AC��
��1����֤��CD��ED
��2��ֱ��д��ͼ�������ǡ�ACD��2���Ľǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
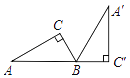
����Ŀ����ͼ��Rt��A'BC'����Rt��ABC��B��˳ʱ����ת���ã��ҵ�A��B��C'��ͬһ��ֱ���ϣ���Rt��ABC�У�����C=90�㣬BC=2��AB=4����Rt��ABC��ת��Rt��A'BC'��ɨ�������Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
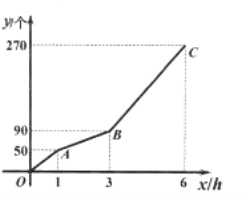
����Ŀ���ס�����̨������ͬ�ӹ�һ�������һ������![]() Сʱ���ڼӹ��������һ��������ֹͣ�������ų����Ϻ��һ�������˹���Ч���ұ��ֲ��䣬�����ӹ��������ڼӹ������й���Ч�ʱ��ֲ��䣮�ס�����̨�����ӹ����������
Сʱ���ڼӹ��������һ��������ֹͣ�������ų����Ϻ��һ�������˹���Ч���ұ��ֲ��䣬�����ӹ��������ڼӹ������й���Ч�ʱ��ֲ��䣮�ס�����̨�����ӹ����������![]() ��������ӹ�ʱ��
��������ӹ�ʱ��![]() ֮��ĺ���ͼ��Ϊ����
֮��ĺ���ͼ��Ϊ����![]() ����ͼ��ʾ��
����ͼ��ʾ��
��1���������һ������ ����������ÿСʱ�ӹ��� ����������һ����ų����Ϻ�ÿСʱ�ӹ��� ���������
��2����![]() ʱ����
ʱ����![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��3���������ӹ������У��ӹ��ʱ��ʱ�������Ҽӹ������������ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƶ��������Ŀ��ٷ�չ�����ڻ������Ĺ�������Ӧ�˶�����Ϊ�˽�ijС������ʹ�ù��������������ij�о�С������ɷø�С����10λ���õ���10λ����һ����ʹ�ù��������Ĵ����ֱ�Ϊ��17��12��15��20��17��0��7��26��17��9��
��1���������ݵ���λ������ ������������ ����
��2��������10λ����һ����ʹ�ù���������ƽ��������
��3������С����200�������Թ��Ƹ�С������һ����ʹ�ù����������ܴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABC��AB��AC����BAC��120�㣬AD��BC�ڵ�D����P��BA�ӳ�����һ�㣬��O���߶�AD��һ�㣬OP��OC�����н��ۣ���ACƽ�֡�PAD������APO����DCO������OPC�ǵȱ������Σ���AC��AO+AP��������ȷ������ǣ�������
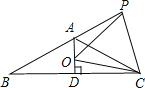
A.�٢ۢ�B.�ڢ�C.�٢ڢ�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2��2��k��1��x+k2=0������ʵ����x1��x2��
��1����k��ȡֵ��Χ��
��2����|x1+x2|=x1x2��1����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����У��ѧ��������������+��������ҵ������һ�ֲ�Ʒ�����ֲ�Ʒ�ɱ���10Ԫ/������֪���ۼ۲����ڳɱ��ۣ�����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����16Ԫ/�����г����鷢�֣��ò�Ʒÿ���������y�����������ۼ�x��Ԫ/����֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����ÿ�����������W��Ԫ�������ۼ�x��Ԫ/����֮��ĺ�����ϵʽ�������ÿ�����ۼ�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com