
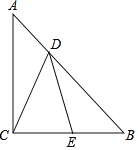
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC.
(1)求证:CD=ED
(2)直接写出图中所有是∠ACD的2倍的角.
【答案】(1)见解析;(2)∠A,∠B,∠CDE是∠ACD的2倍的角
【解析】
(1)由“SAS”可证△ADC≌△BED;
(2)由全等三角形的性质可得∠ACD=∠BDE,CD=DE,由外角性质和等腰三角形的性质可求∠DCE=67.5°,即可求解.
解:(1)∵AC=BC,∠ACB=90°,
∴∠A=∠B=45°,且AD=BE,BD=AC,
∴△ADC≌△BED(SAS),
∴CD=DE.
(2)∵△ADC≌△BED,
∴∠ACD=∠BDE,CD=DE,
∵∠BDC=∠A+∠ACD=∠CDE+∠BDE,
∴∠CDE=∠A=45°,且DC=DE,
∴∠DCE=67.5°,
∴∠ACD=∠ACB﹣∠DCE=22.5°,
∵∠A=∠B=∠CDE=45°,
∴∠A,∠B,∠CDE是∠ACD的2倍的角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商店将进价为100元的某商品按120元的价格出售,可卖出300个;若商店在120元的基础上每涨价1元,就要少卖10个,而每降价1元,就可多卖30个.
(1)求所获利润y (元)与售价x(元)之间的函数关系式;
(2)为获利最大,商店应将价格定为多少元?
(3)为了让利顾客,且获利最大,商店应将价格定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
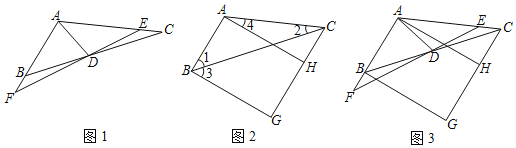
【题目】(1)如图1,在△ABC中,D是BC的中点,过D点画直线EF与AC相交于E,与AB的延长线相交于F,使BF=CE.
①已知△CDE的面积为1,AE=kCE,用含k的代数式表示△ABD的面积为 ;
②求证:△AEF是等腰三角形;
(2)如图2,在△ABC中,若∠1=2∠2,G是△ABC外一点,使∠3=∠1,AH∥BG交CG于H,且∠4=∠BCG﹣∠2,设∠G=x,∠BAC=y,试探究x与y之间的数量关系,并说明理由;
(3)如图3,在(1)、(2)的条件下,△AFD是锐角三角形,当∠G=100°,AD=a时,在AD上找一点P,AF上找一点Q,FD上找一点M,使△PQM的周长最小,试用含a、k的代数式表示△PQM周长的最小值 .(只需直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
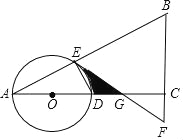
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,以OA为半径的圆分别交AB、AC于点E、D,在BC的延长线上取点F,使得BF=EF.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若∠A=30°,求证:DG=![]() DA;
DA;
(3)若∠A=30°,且图中阴影部分的面积等于2![]() ,求⊙O的半径的长.
,求⊙O的半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.则这根芦苇的长度是( )

A. 10尺 B. 11尺 C. 12尺 D. 13尺
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,4a),B(3a,0),△AOB的面积是150.
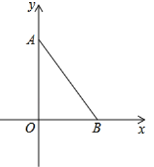
(1)求点A的坐标;
(2)点P是射线AB上的一点,点P的横坐标为t,连接PO,若△PBO的面积为S,试用含有t的式子表示S.
(3)在(2)的条件下,若点P在第一象限内,且S△PBO=126,过P作PE⊥AB,交y轴于点D,交x轴于点E,且OB=OD,连接AE,M为AE上一点,连接OM交PE于点N,若∠EMN+∠ABE=180°,求点N的坐标.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的内接四边形
的内接四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上.
上.
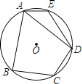
(1)求![]() 的度数;
的度数;
(2)若![]() 的半径为
的半径为![]() ,则
,则![]() 的长为多少?
的长为多少?
(3)连接![]() ,
,![]() ,当
,当![]() 时,
时,![]() 恰好是
恰好是![]() 的内接正
的内接正![]() 边形的一边,求
边形的一边,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将直角三角板ABC按如图1放置,直角顶点C与坐标原点重合,直角边AC、BC分别与x轴和y轴重合,其中∠ABC=30°.将此三角板沿y轴向下平移,当点B平移到原点O时运动停止.设平移的距离为m,平移过程中三角板落在第一象限部分的面积为s,s关于m的函数图象(如图2所示)与m轴相交于点P(![]() ,0),与s轴相交于点Q.
,0),与s轴相交于点Q.
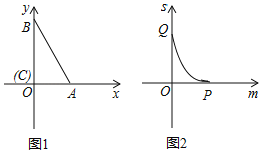
(1)试确定三角板ABC的面积;
(2)求平移前AB边所在直线的解析式;
(3)求s关于m的函数关系式,并写出Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com