
【题目】某商店将进价为100元的某商品按120元的价格出售,可卖出300个;若商店在120元的基础上每涨价1元,就要少卖10个,而每降价1元,就可多卖30个.
(1)求所获利润y (元)与售价x(元)之间的函数关系式;
(2)为获利最大,商店应将价格定为多少元?
(3)为了让利顾客,且获利最大,商店应将价格定为多少元?
【答案】(1)![]() ;(2)售价定为115元获得最大为6750元;(3)115元
;(2)售价定为115元获得最大为6750元;(3)115元
【解析】
(1)以120元为基础,当涨价时,大于120元,当降价时,小于120元,利用每个商品的利润×卖出数量=总利润分别写出函数关系式即可;
(2)利用配方法求得两个函数解析式的最大值,比较得出答案;
(3)分别求出函数最值进而得出答案.
解:(1)当x>120时,
y1=﹣10x2+2500x﹣150000;
当100<x<120时,
y2=﹣30x2+6900x﹣390000,
即![]() ;
;
(2)y1=﹣10x2+2500x﹣150000=﹣10(x﹣125)2+6250;
y2=﹣30x2+6900x﹣390000=﹣30(x﹣115)2+6750;
∵6750>6250,
∴当售价定为115元时,获得最大为6750元;
(3)由(2)可知,
当涨价x=5(元)时,所获利润y1的最大值=6250(元);
当降价x=5(元)时,所获利润y2的最大值=6750(元).
∴为获利最大,应降价5元,即将价格定为115元.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,∠B=30°,以点 A 为圆心,任意长为半径画弧分别交 AB,AC 于点M 和 N,再分别以 M,N 为圆心,大于![]() 的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2.正确的是( ).
的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2.正确的是( ).
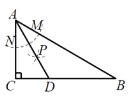
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=10,BC=12,E为DC的中点,连接BE,作AF⊥BE,垂足为F.

(1)求证:△BEC∽△ABF;
(2)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
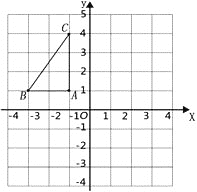
【题目】如图,在平面直角坐标系中,已知 ![]() ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
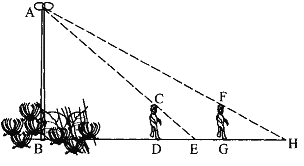
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
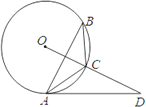
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形例如:某三角形三边长分别是5,6和8,因为![]() ,所以这个三角形是常态三角形.
,所以这个三角形是常态三角形.
(1)若△ABC三边长分别是2,![]() 和4,则此三角形 常态三角形(填“是”或“不是”);
和4,则此三角形 常态三角形(填“是”或“不是”);
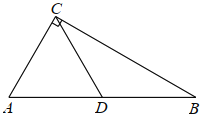
(2)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,CD=![]() AB, 若△ACD是常态三角形,求△ABC的面积;,
AB, 若△ACD是常态三角形,求△ABC的面积;,
(3)若Rt△ABC是常态△,斜边是![]() ,则此三角形的两直角边的和= .
,则此三角形的两直角边的和= .
查看答案和解析>>
科目:初中数学 来源: 题型:
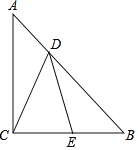
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC.
(1)求证:CD=ED
(2)直接写出图中所有是∠ACD的2倍的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com