
����Ŀ�������¶���һ��������:����ƽ���͵��ڵ�����ƽ����4���������ν�����̬����������:ij���������߳��ֱ���5��6��8����Ϊ![]() ����������������dz�̬������.
����������������dz�̬������.
(1)����ABC���߳��ֱ���2��![]() ��4����������� ��̬������(������������������);
��4����������� ��̬������(������������������);
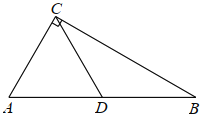
(2)��ͼ��Rt��ABC�У���ACB=90����BC=6����DΪAB���е㣬����CD��CD=![]() AB�� ����ACD�dz�̬�����Σ����ABC�����;��
AB�� ����ACD�dz�̬�����Σ����ABC�����;��
(3)��Rt��ABC�dz�̬����б����![]() ����������ε���ֱ�DZߵĺ�= .
����������ε���ֱ�DZߵĺ�= .
���𰸡�(1)�ǣ�(2)![]() ��
��![]() ��(3) 2
��(3) 2![]() +4.
+4.
��������
��1��ֱ�����ó�̬�����εĶ����жϼ��ɣ�
��2����CD=AD=BD=x�����ù��ɶ������AC2=4x2-36��Ȼ����ݳ�̬�����εĶ��������з������x�������ɵ�AC�ij���������������������ʽ��⣻
��3���ɹ��ɶ����ͳ�̬�����εĶ���ã�a2+b2=c2��a2+c2=4b2�����a��b=![]() ��Ȼ����δ֪����ʾ��c�ij����������a��b�ij��������ó��𰸣�
��Ȼ����δ֪����ʾ��c�ij����������a��b�ij��������ó��𰸣�
(1)��![]() ��
��
����������dz�̬�����Σ�
��2����Rt��ABC�У���ACB=90����BC=6����DΪAB���е㣬
��CD=AD=BD=![]() AB��
AB��
��CD=AD=BD=![]() AB=x����AB=2x��
AB=x����AB=2x��
�ɹ��ɶ����ã�AC2+62=��2x��2��
��AC2=4x2-36��
�١ߡ�ACD�dz�̬�����Σ�
��CD2+AD2=4AC2��
��x2+x2=4��4x2-36����
��x2=![]() ��
��
��AC2=![]()
��AC=![]() ��
��
���ABC�������![]() ��AC��BC=
��AC��BC=![]() ��
��
�ڡߡ�ACD�dz�̬�����Σ�
��CD2+AC2=4AD2��
��x2+AC2=4x2��
��AC2=3x2��
�ɵ�![]() ��
��
��ã�x=6��
��AC=![]() ��
��
���ABC�������![]() ��AC��BC=
��AC��BC=![]() ��
��
������������ABC�����Ϊ![]() ��
��![]() ��
��
��3����Rt��ABC�dz�̬�����Σ�
������ֱ�DZ߷ֱ�Ϊ��a��b��б��Ϊc��
���ɹ��ɶ����ͳ�̬�����εĶ���ã�a2+b2=c2��a2+c2=4b2��
��2a2=3b2��
��a��b=![]() ��
��
��a=![]() x��b=
x��b=![]() x��
x��
��c=![]() x��
x��
�����2![]() ����
����![]() ��
��
��ã�x=![]() ��
��
��a+b=![]() .
.


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
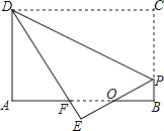
����Ŀ����ͼ������ֽƬABCD��AB=5��BC=3����P��BC���ϣ�����CDP��DP�۵�����C���ڵ�E����PE��DE�ֱ�AB�ڵ�O��F����OP=OF����AF��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵꽫����Ϊ100Ԫ��ij��Ʒ��120Ԫ�ļ۸���ۣ�������300�������̵���120Ԫ�Ļ�����ÿ�Ǽ�1Ԫ����Ҫ����10������ÿ����1Ԫ���Ϳɶ���30����
��1������������y ��Ԫ�����ۼ�x��Ԫ��֮��ĺ�����ϵʽ��
��2��Ϊ��������̵�Ӧ���۸�Ϊ����Ԫ��
��3��Ϊ�������˿ͣ��һ�������̵�Ӧ���۸�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ��,��CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD.

��1����֤��CDΪ��O�����ߣ�
��2����CD=2AD����O��ֱ��Ϊ10�����߶�AB�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����1����![]() �����
�����![]() ���ٻ�
���ٻ�![]() ��ƽ����
��ƽ����![]() �����߹���ͼ��
�����߹���ͼ��
��2����![]() ������������֤����
������������֤����
��֪��![]() �У�
��![]() ��
��![]() �����
�����![]() ��ƽ���ߣ�
��ƽ���ߣ�
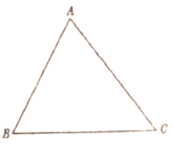
��֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
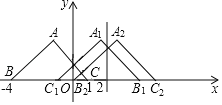
����Ŀ����ͼ����ABC�У���A��90����AB��AC������BΪ����4��0��������CΪ��1��0��������ABC����y����ԳƱ任�õ���A1B1C1���ٽ���A1B1C1����ֱ��x��2��������2��0����ֱ��x���ֱ�ߣ���ԳƱ任�õ���A2B2C2���ٽ���A2B2C2����ֱ��x��4��ԳƱ任�õ���A3B3C3���ٽ���A3B3C3����ֱ��x��6��ԳƱ任�õ���A4B4C4�������˹��ɼ����任��ȥ�����A10������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
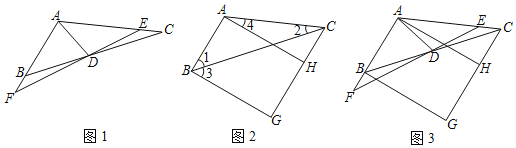
����Ŀ����1����ͼ1������ABC�У�D��BC���е㣬��D�㻭ֱ��EF��AC�ཻ��E����AB���ӳ����ཻ��F��ʹBF��CE��
����֪��CDE�����Ϊ1��AE��kCE���ú�k�Ĵ���ʽ��ʾ��ABD�����Ϊ�� ����
����֤����AEF�ǵ��������Σ�
��2����ͼ2������ABC�У�����1��2��2��G����ABC��һ�㣬ʹ��3����1��AH��BG��CG��H���ҡ�4����BCG����2�����G��x����BAC��y����̽��x��y֮���������ϵ����˵�����ɣ�
��3����ͼ3���ڣ�1������2���������£���AFD����������Σ�����G��100����AD��aʱ����AD����һ��P��AF����һ��Q��FD����һ��M��ʹ��PQM���ܳ���С�����ú�a��k�Ĵ���ʽ��ʾ��PQM�ܳ�����Сֵ�� ������ֻ��ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
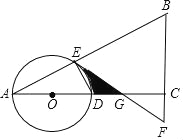
����Ŀ����ͼ������ABC�У���ACB=90�㣬O�DZ�AC��һ�㣬��OΪԲ�ģ���OAΪ�뾶��Բ�ֱ�AB��AC�ڵ�E��D����BC���ӳ�����ȡ��F��ʹ��BF=EF��
��1���ж�ֱ��EF���O��λ�ù�ϵ����˵�����ɣ�
��2������A=30������֤��DG=![]() DA��
DA��
��3������A=30������ͼ����Ӱ���ֵ��������2![]() �����O�İ뾶�ij���
�����O�İ뾶�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ�����ǰ�ABC����ͼ1���ã�ֱ�Ƕ���C������ԭ���غϣ�ֱ�DZ�AC��BC�ֱ���x���y���غϣ����С�ABC��30�����������ǰ���y������ƽ�ƣ�����Bƽ�Ƶ�ԭ��Oʱ�˶�ֹͣ����ƽ�Ƶľ���Ϊm��ƽ�ƹ��������ǰ����ڵ�һ�����ֵ����Ϊs��s����m�ĺ���ͼ����ͼ2��ʾ����m���ཻ�ڵ�P��![]() ��0������s���ཻ�ڵ�Q��
��0������s���ཻ�ڵ�Q��
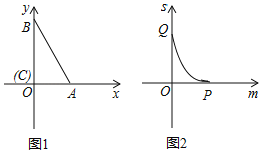
��1����ȷ�����ǰ�ABC�������
��2����ƽ��ǰAB������ֱ�ߵĽ���ʽ��
��3����s����m�ĺ�����ϵʽ����д��Q������꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com