
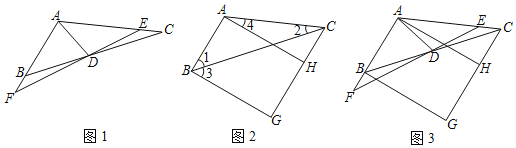
【题目】(1)如图1,在△ABC中,D是BC的中点,过D点画直线EF与AC相交于E,与AB的延长线相交于F,使BF=CE.
①已知△CDE的面积为1,AE=kCE,用含k的代数式表示△ABD的面积为 ;
②求证:△AEF是等腰三角形;
(2)如图2,在△ABC中,若∠1=2∠2,G是△ABC外一点,使∠3=∠1,AH∥BG交CG于H,且∠4=∠BCG﹣∠2,设∠G=x,∠BAC=y,试探究x与y之间的数量关系,并说明理由;
(3)如图3,在(1)、(2)的条件下,△AFD是锐角三角形,当∠G=100°,AD=a时,在AD上找一点P,AF上找一点Q,FD上找一点M,使△PQM的周长最小,试用含a、k的代数式表示△PQM周长的最小值 .(只需直接写出结果)
【答案】(1)①k+1;②见解析;(2)y=![]() x+45°,理由见解析;(3)
x+45°,理由见解析;(3)![]()
【解析】
(1)①先根据AE与CE之比求出△ADE的面积,进而求出ADC的面积,而D中BC中点,所以△ABD面积与△ADC面积相等;②延长BF至R,使FR=BF,连接RC,注意到D是BC中点,过B过B点作BG∥AC交EF于G.得![]() ,再利用等腰三角形性质和判定即可解答;
,再利用等腰三角形性质和判定即可解答;
(2)设∠2=α.则∠3=∠1=2∠2=2α,根据平行线性质及三角形外角性质可得∠4=α,再结合三角形内角和等于180°联立方程即可解答;
(3)分别作P点关于FA、FD的对称点P'、P',则PQ+QM+PM=P'Q+QM+MP“≥P'P'=FP,当FP垂直AD时取得最小值,即最小值就是AD边上的高,而AD已知,故只需求出△ADF的面积即可,根据AE=kEC,AE=AF,CE=BF,可以将△ADF的面积用k表示出来,从而问题得解.
解:(1)
①∵AE=kCE,
∴S△DAE=kS△DEC,
∵S△DEC=1,
∴S△DAE=k,
∴S△ADC=S△DAE+S△DEC=k+1,
∵D为BC中点,
∴S△ABD=S△ADC=k+1.
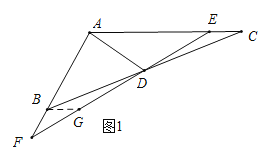
②如图1,过B点作BG∥AC交EF于G.
∴![]() ,
,![]()
在△BGD和△CED中,
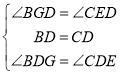 ,
,
∴![]() (ASA),
(ASA),
∴BG=CE,
又∵BF=CE,
∴BF=BG,
∴![]() ,
,
∴![]()
∴AF=AE,即△AEF是等腰三角形.
(2)如图2,设AH与BC交与点N,∠2=α.
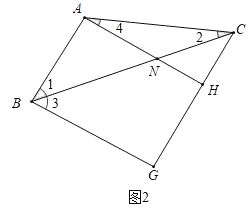
则∠3=∠1=2∠2=2α,
∵AH∥BG,
∴∠CNH=∠ANB=∠3=2α,
∵∠CNH=∠2+∠4,
∴2α=α+∠4,
∴∠4=α,
∵∠4=∠BCG﹣∠2,
∴∠BCG=∠2+∠4=2α,
在△BGC中,![]() ,即:
,即:![]() ,
,
在△ABC中,![]() ,即:
,即:![]() ,
,
联立消去![]() 得:y=
得:y=![]() x+45°.
x+45°.
(3)如图3,作P点关于FA、FD的对称点P'、P',
连接P'Q、P'F、PF、P'M、P'F、P'P',
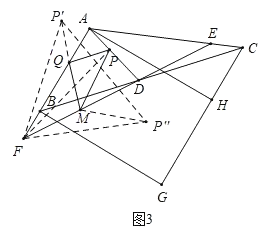
则FP'=FP=FP',PQ=P'Q,PM=P'M,∠P'FQ=∠PFQ,∠P'FM=∠PFM,
∴∠P'FP'=2∠AFD,
∵∠G=100°,
∴∠BAC=![]() ∠G+45°=120°,
∠G+45°=120°,
∵AE=AF,
∴∠AFD=30°,
∴∠P'FP'=2∠AFD=60°,
∴△FP'P'是等边三角形,
∴P'P'=FP'=FP,
∴PQ+QM+PM=P'Q+QM+MP'≥P'P'=FP,
当且仅当P'、Q、M、P'四点共线,且FP⊥AD时,△PQM的周长取得最小值.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 的周长最小值为
的周长最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=10,BC=12,E为DC的中点,连接BE,作AF⊥BE,垂足为F.

(1)求证:△BEC∽△ABF;
(2)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
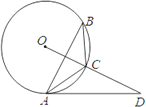
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形例如:某三角形三边长分别是5,6和8,因为![]() ,所以这个三角形是常态三角形.
,所以这个三角形是常态三角形.
(1)若△ABC三边长分别是2,![]() 和4,则此三角形 常态三角形(填“是”或“不是”);
和4,则此三角形 常态三角形(填“是”或“不是”);
(2)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,CD=![]() AB, 若△ACD是常态三角形,求△ABC的面积;,
AB, 若△ACD是常态三角形,求△ABC的面积;,
(3)若Rt△ABC是常态△,斜边是![]() ,则此三角形的两直角边的和= .
,则此三角形的两直角边的和= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P是边BC上的中点,PD⊥AB,PE⊥AC,垂足分别为点D、E.
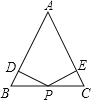
(1)求证:PD=PE;
(2)若AB=6cm,∠BAC=30°,请直接写出PD+PE= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BAC中,∠B和∠C的平分线相交于点F,过点F作DE∥BC交AB于点D,交AC于点E,若BD=5,CE=4,则线段DE的长为( )
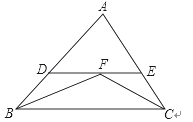
A. 9 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
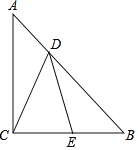
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC.
(1)求证:CD=ED
(2)直接写出图中所有是∠ACD的2倍的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下列结论:①AC平分∠PAD;②∠APO=∠DCO;③△OPC是等边三角形;④AC=AO+AP;其中正确的序号是( )
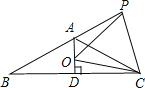
A.①③④B.②③C.①②④D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com