
【题目】如图,在![]() 的内接四边形
的内接四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上.
上.
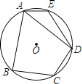
(1)求![]() 的度数;
的度数;
(2)若![]() 的半径为
的半径为![]() ,则
,则![]() 的长为多少?
的长为多少?
(3)连接![]() ,
,![]() ,当
,当![]() 时,
时,![]() 恰好是
恰好是![]() 的内接正
的内接正![]() 边形的一边,求
边形的一边,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)12.
;(3)12.
【解析】
(1)连接BD,根据圆的内接四边形的性质得出∠BAD的度数,由AB=AD,可证得△ABD是等边三角形,求得∠ABD=60°,再利用圆的内接四边形的性质,即可求得∠AED的度数;
(2)连接OA,由圆周角定理求出∠AOD的度数,由弧长公式即可得出![]() 的长;
的长;
(3)首先连接OA,由∠ABD=60°,利用圆周角定理,即可求得∠AOD的度数,继而求得∠AOE的度数,即可得出结果.
(1)连接![]() ,如图
,如图![]() 所示:
所示:
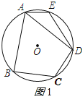
∵四边形![]() 是
是![]() 的内接四边形,
的内接四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵四边形![]() 是
是![]() 的内接四边形,
的内接四边形,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() 的长
的长![]() ;
;
(3)连接![]() ,如图
,如图![]() 所示:
所示:
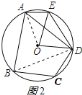
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
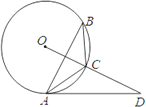
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
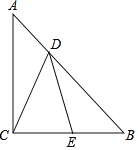
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC.
(1)求证:CD=ED
(2)直接写出图中所有是∠ACD的2倍的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将![]() 个棱长为
个棱长为![]() (单位:
(单位:![]() )的正方体,摆成
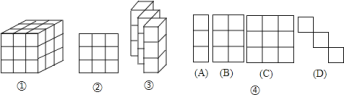
)的正方体,摆成![]() 的大正方体(如图①),从上面、正面、左面看到的大正方体的正投影图都是如图②,是
的大正方体(如图①),从上面、正面、左面看到的大正方体的正投影图都是如图②,是![]() 的正方形.
的正方形.
(1)如果将图①中,左前方的![]() 个正方体和右后方的
个正方体和右后方的![]() 个正方体取走,就变成图③.这时从正面、左面、上面看的正投影图依次是图④中的________;
个正方体取走,就变成图③.这时从正面、左面、上面看的正投影图依次是图④中的________;
(2)在图③中,至少要补防________个正方体后,组成的立体图形,从上面看的正投影图是图②.
查看答案和解析>>
科目:初中数学 来源: 题型:
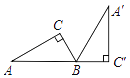
【题目】如图,Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则Rt△ABC旋转到Rt△A'BC'所扫过的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
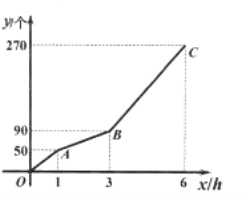
【题目】甲、乙两台机器共同加工一批零件,一共用了![]() 小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数
小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数![]() (个)与甲加工时间
(个)与甲加工时间![]() 之间的函数图象为折线
之间的函数图象为折线![]() ,如图所示.
,如图所示.
(1)这批零件一共有 个,甲机器每小时加工 个零件,乙机器排除故障后每小时加工 个零件;
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(3)在整个加工过程中,甲加工多长时间时,甲与乙加工的零件个数相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下列结论:①AC平分∠PAD;②∠APO=∠DCO;③△OPC是等边三角形;④AC=AO+AP;其中正确的序号是( )
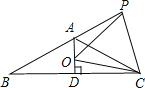
A.①③④B.②③C.①②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:如图(1),在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为筝形.
(1)写出筝形的两个性质(定义除外).
① ;② .
(2)如图(2),在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形.
(3)如图(3),在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com