
����Ŀ����ͼ����ABC�У���B=90����AB=12��BC=16����P�ӵ�A��ʼ�ر�AB���B��1cm/s���ٶ��ƶ������ͬʱ����Q�ӵ�B��ʼ�ر�BC���C��2cm/s���ٶ��ƶ������P��Q�ֱ��A��Bͬʱ����������Q�˶�����Cʱ������ֹͣ�˶����ʣ�
��1�������������PBQ���������20cm2��
��2����PBQ������������ABC�������һ�������ᣬ�������ʱ���˶�ʱ�䣻�����ᣬ��˵������.
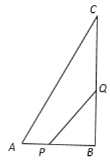
���𰸡���1���ʾ���2�����PBQ���������20 cm2����2�����ᣬ������
��������
��1���辭��t���PBQ���������20cm2�����������ε������ʽ�������������⼴�ɣ�
��2������������֮��������ϵ�������������⼴�ɣ�
�⣺��1���������
AP=t��BP=12-t��BQ=2t
��![]()
��ã�t1=2��t2=10
��BQ=2t��BC=16
��t��8
��t2=10��ȥ
�ʾ���2�����PBQ���������20cm2��
��2������
���ɣ�����PBQ������������ABC�������һ�룬��
![]()
��![]() ��
��
�ߡ�=122-4��48<0��������ʵ����
�����PBQ��������������ABC�������һ�룮


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ļ���˾ΪijѧУ�����ס�������Ʒ�Ƶ��������ģ���Ʒ����A��B��C�����ͺţ���Ʒ����D��E�����ͺţ���Ҫ�Ӽס�������Ʒ�Ƶ������и�ѡ��һ���ͺŽ��о�����
��1�������¼��Dz������¼����� ��
A��ѡ����Ʒ�Ƶ�D�ͺ� B����ѡ����Ʒ��Ҳѡ����Ʒ��
C��ѡ����Ʒ�Ƶ�A�ͺź���Ʒ�Ƶ�D�ͺ� D��ֻѡ����Ʒ�Ƶ�A�ͺ�
��2��д�����е�ѡ�����������б�������״ͼ����
��3�����������ѡ�������У�ÿ�ַ�����ѡ�еĿ�������ͬ����ôA�����ı�ѡ�еĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4����ȫ��ͬ��С�ֱ��������1��2��3��4��������һ������������ת��Բ�̣����ֳ������ȵ�3���������ֱ��������1��2��3����ͼ��ʾ����

��1���ӿڴ�������һ��С���������ϵ����ִ���2�ĸ���Ϊ ��
��2��С����С����ͨ����Ϸ������˭����ѧУ�μӸ�ӽ��������Ϸ����Ϊ��һ�˴ӿڴ�������һ��С����һ��ת��Բ�̣�����������ϵ�������Բ����ת������֮��С��5����ôС��ȥ������С��ȥ������Ϊ��Ϸ��ƽ��������״ͼ���б���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
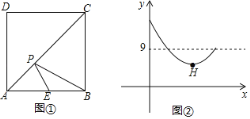
����Ŀ����ͼ������������ABCD�У���E��AB���е㣬��P�ǶԽ���AC��һ���㣬��PC�ij���Ϊx��PE��PB�ij��Ⱥ�Ϊy��ͼ����y����x�ĺ���ͼ����ͼ������͵�H������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������![]() ������
������![]() �͵�
�͵�![]() ��
��
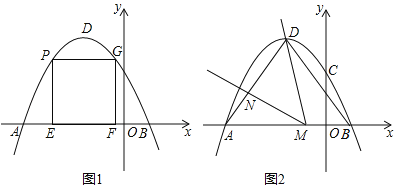
(1)�������ߵĽ���ʽ������![]() �����ꣻ
�����ꣻ
(2)��![]() ����������
����������![]() ��
��![]() ֮���һ�㣬����
֮���һ�㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() �ᣬ���������ڵ�
�ᣬ���������ڵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��������
��������![]() ���ܳ����ʱ�����
���ܳ����ʱ�����![]() �ĺ����ꣻ
�ĺ����ꣻ
(3)��ͼ2������![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() ��(����
��(����![]() ��
��![]() �غ�)����
�غ�)����![]() ��
��![]() ���߶�
���߶�![]() �ڵ�
�ڵ�![]() ���Ƿ����������
���Ƿ����������![]() ��ʹ��
��ʹ��![]() Ϊ���������Σ������ڣ����
Ϊ���������Σ������ڣ����![]() �ij����������ڣ���˵�����ɣ�
�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
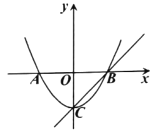
����Ŀ����ͼ����֪����Ϊ![]() ��������
��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() ��
��
��1�����![]() �����ꣻ
�����ꣻ
��2������κ���![]() �Ľ���ʽ��
�Ľ���ʽ��
��3����ֱ��![]() ����������
����������![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() �����꣺�������ڣ���˵�����ɣ�
�����꣺�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A����BCΪֱ������O��һ�㣬I����ABC�����ģ�AI���ӳ��߽���O�ڵ�D������D��BC��ƽ���߽�AB��AC���ӳ�����E��F������˵�����١�DBC�ǵ���ֱ�������Σ���EF����O���У���EF=2BC������B��I��C���Ե�D ΪԲ�ĵ�ͬһ��Բ�ϣ�����һ����ȷ����_______��������Ϊ��ȷ���۵���Ŷ����ϣ�
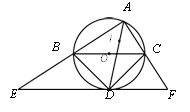
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0 ��4a+2b+c��0 ��4ac��b2��8a ��![]() ��a��
��a��![]() ��b��c�����к�������ȷ���۵�ѡ���ǣ�������
��b��c�����к�������ȷ���۵�ѡ���ǣ�������

A. �٢� B. �٢ۢ� C. �ڢܢ� D. �٢ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У���
�У���![]() �͵�
�͵�![]() �ǶԽ���
�ǶԽ���![]() �ϵ����㣬
�ϵ����㣬![]()
![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
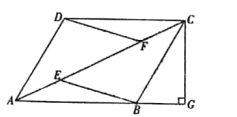
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2����![]() ��
��![]() ��BC=4
��BC=4![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com