
分析 (1)直接求出△的值,进而得出k的取值范围;
(2)令y=0,直接解方程得出符合题意的k的值;
(3)首先求出A,B点坐标,进而表示出A′,B′点坐标,再表示出平移后解析式,进而得出n的取值范围.
解答 (1)证明:△=(4k+1)2-4k(3k+3)=(2k-1)2,
∵二次函数有两个不重合的零点,
∴2k-1≠0,即k≠$\frac{1}{2}$,
∵k≠0,
∴当k≠0且k≠$\frac{1}{2}$时,二次函数有两个不重合的零点;
(2)解:当y=0,则0=kx2-(4k+1)x+3k+3,
解方程得:x=$\frac{(4k+1)±\sqrt{(2k-1)^{2}}}{2k}$,
∴x=3或x=1+$\frac{1}{k}$,
∵函数的两个零点都是整数,k是整数,
∴$\frac{1}{k}$是整数.
∴k=±1;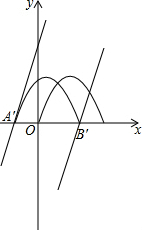
(3)解:∵k<0,
∴k=-1.
∴y=-x2+3x,y=4x+3.
∵函数的两个零点分别是A,B(点A在点B的左侧),
∴A(0,0),B(3,0).
∴平移后的点为:A′(-n,0),B′(3-n,0).
平移后的解析式为:y=4x+3+n.
∴-4n+3+n=0,
解得:n=1,
4(3-n)+3+n=0,
解得:n=5,
∴1≤n≤5.
点评 本题考查了二次函数和一次函数的性质,平移的性质,根的判别式等知识点的应用,通过做此题培养了学生的分析问题和解决问题的能力,题目综合性比较强,有一定的难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
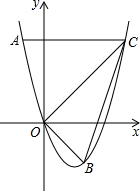 如图,二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m).
如图,二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
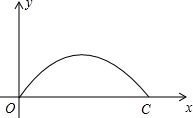 如图,庄子大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需( )
如图,庄子大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需( )| A. | 18秒 | B. | 36秒 | C. | 38秒 | D. | 46秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com