(1)解:

,
解得:
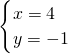
,
即:A(4,-1),
当y=0时,y=

x-3=0,
x=6,
∴D(6,0),
当x=0时,y=-x+3=3,
∴C(0,3),
设经过A,C,D三点的抛物线函数解析式是y=ax
2+bx+c,
把A(4,-1)C(0,3),D(6,0)代入并解得:a=

,b=-2,c=3,
∴抛物线的解析式是

,
答:点A的坐标是(4,-1),经过A,C,D三点的抛物线函数解析式是y=

x
2-2x+3.
(2)新的抛物线

,
可以,因为过A,B,E的抛物线解析式为

=-

(x-

)
2+

,
顶点为

,可以把抛物线

先以x轴为对称轴做轴对称变换,则解析式为

=-

(x-4)
2+2,
然后向左平移

个单位,最后向上平移

个单位.
答:新的抛物线的解析式是:

,可以,变换的过程是先以x轴为对称轴做轴对称变换,
然后向左平移

个单位,最后向上平移

个单位.
(3)存在,因为A点是抛物线的顶点,
所以∠PAQ小于90度,必不可能等于∠BAD(这个角是钝角)
所以要使△APQ与△ABD相似,只要使∠PAQ等于∠ABD或者∠ADB,
就可以存在,
设抛物线对称轴与x轴交点为M,直线AQ与x轴交点为N,
则当∠PAQ=∠ABD时,△AMN≌△ABM,
所以N坐标为(5,0),
直线AQ解析式为y=x-5,
与抛物线的交点Q为(8,3),
此时AP=12或

,
当∠PAQ=∠ADB时,△AMN∽△AND,
所以N坐标为(

,0),
直线AQ解析式为y=2x-9,
与抛物线的交点Q为(12,15),
此时AP=24或

.
答:动点Q的坐标是(8,3)或(12,15),AP的长度是12或

或24或

.
分析:(1)解直线I
1和直线I
2组成的方程组,即可求出A的坐标,把y=o,x=0,分别代入直线1
1和直线I
2即可求出D、C的坐标,设经过A,C,D三点的抛物线函数解析式是y=ax
2+bx+c,代入坐标即可求出解析式;
(2)根据坐标设出解析式就能写出解析式,先以x轴为对称轴做轴对称变换,然后向左平移,最后向下平移即可;
(3)①当∠PAQ=∠ABD时,△AMN≌△ABM,求出Q的坐标,进一步求出AP的长,②当∠PAQ=∠ADB时,△AMN∽△AND,求出Q的坐标,进一步求出AP的长.
点评:本题主要考查了二次函数图象上点的坐标特征,用待定系数法求二次函数的解析式,图形的平移和旋转,相似三角形的旋转和判定等知识点,综合运用性质进行计算是解此题的关键.

 的图象交于A点,l1与坐
的图象交于A点,l1与坐 标轴分别交于B,C两点,l2与坐标轴分别交于D,E两点.
标轴分别交于B,C两点,l2与坐标轴分别交于D,E两点. ,
,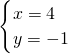 ,
, x-3=0,
x-3=0, ,b=-2,c=3,
,b=-2,c=3, ,
, x2-2x+3.
x2-2x+3. ,
, =-
=- (x-
(x- )2+
)2+ ,
, ,可以把抛物线
,可以把抛物线
 =-
=- (x-4)2+2,
(x-4)2+2, 个单位,最后向上平移
个单位,最后向上平移 个单位.
个单位. ,可以,变换的过程是先以x轴为对称轴做轴对称变换,
,可以,变换的过程是先以x轴为对称轴做轴对称变换, 个单位,最后向上平移
个单位,最后向上平移 个单位.
个单位. ,
, ,0),
,0), .
. 或24或
或24或 .
.

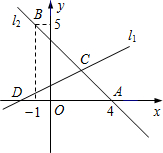 l2交于点C.
l2交于点C. 如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.