
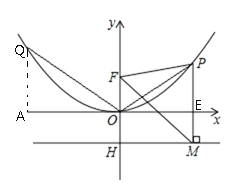
【题目】二次函数图象的顶点在原点O,且过点(1,1),点F(0,![]() )在y轴上,直线
)在y轴上,直线![]() 与y轴交于点H,
与y轴交于点H,
(1)求二次函数的解析式;
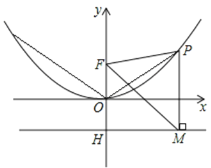
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线![]() 交于点M,求证:FM平分∠OFP;
交于点M,求证:FM平分∠OFP;
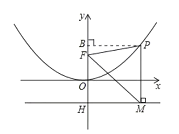
(3)当点P横坐标为![]() 时,过O点作OQ⊥OP交抛物线于点Q,在y轴上找点C,使△OCQ是以OQ为腰的等腰三角形,求点C的坐标.
时,过O点作OQ⊥OP交抛物线于点Q,在y轴上找点C,使△OCQ是以OQ为腰的等腰三角形,求点C的坐标.
【答案】(1)y=x2;(2)见解析(3)C点坐标为(0,![]() )或(0,-
)或(0,-![]() )或(0,1).
)或(0,1).
【解析】
(1)根据题意可设函数的解析式为y=ax2,将点(1,1)代入函数解析式,求出a的值,继而可求得二次函数的解析式;
(2)过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,∠PFM=∠PMF,结合平行线的性质,可得出结论;
(3)先求出P(![]() ,2),得到OE=
,2),得到OE=![]() ,PE=2,过点Q作QA⊥x轴与点A,根据OP⊥OQ,利用tan∠POE= tan∠AQO求出OA=
,PE=2,过点Q作QA⊥x轴与点A,根据OP⊥OQ,利用tan∠POE= tan∠AQO求出OA=![]() QA,设Q(a,a2)代入二次函数得到Q点坐标,故得到OQ的长,再根据当△OCQ是以OQ为腰的等腰三角形分①当OQ=OC时与②当OQ=CQ时分别进行求解.
QA,设Q(a,a2)代入二次函数得到Q点坐标,故得到OQ的长,再根据当△OCQ是以OQ为腰的等腰三角形分①当OQ=OC时与②当OQ=CQ时分别进行求解.
(1)解:∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将(1,1)代入y=ax2得:a=1,
∴二次函数的解析式为y=x2;
(2)证明:∵点P在抛物线y=x2上,
∴可设点P的坐标为(x,x2),
过点P作PB⊥y轴于点B,
则BF=| x2![]() |,PB=|x|,
|,PB=|x|,
∴Rt△BPF中,
PF=![]() =
=![]() ,
,
∵PM⊥直线![]() ,
,
∴PM=![]() ,
,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)当x=![]() 时,y=
时,y=![]() ,
,
∴P(![]() ,2)
,2)
设OM与x轴交于E点,
∴OE=![]() ,PE=2,
,PE=2,
过点Q作QA⊥x轴与点A,
∵OP⊥OQ,
∴∠QOP=90°
∴∠AQO+∠QOA=90°=∠QOA+∠POE,
∴∠POE=∠AQO
∴tan∠POE= tan∠AQO=![]() =
=![]()
∴OA=![]() QA
QA
设Q(a,a2),∴-a=![]() a2,
a2,
解得a1=0(舍去),a2=-![]()
∴Q(-![]() ,
,![]() )
)
∴QO=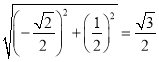
当△OCQ是以OQ为腰的等腰三角形,
∴①当OQ=OC时,即C点为(0,![]() )或(0,-
)或(0,-![]() )
)
②当OQ=CQ时,设C(0,c)则![]() =
=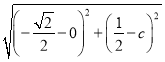
解得,c1=1,c2=0(舍去),
∴C(0,1)
综上:C点坐标为(0,![]() )或(0,-
)或(0,-![]() )或(0,1).
)或(0,1).


科目:初中数学 来源: 题型:
【题目】如图,要用篱笆(虚线部分)成一个矩形苗圃![]() ,其中两边靠的墙足够长,中间用平行于
,其中两边靠的墙足够长,中间用平行于![]() 的篱笆
的篱笆![]() 隔开,已知篱笆的总长度为18米,设矩形苗圃
隔开,已知篱笆的总长度为18米,设矩形苗圃![]() 的一边
的一边![]() 的长为
的长为![]() ,矩形苗圃
,矩形苗圃![]() 面积为
面积为![]() .
.

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求所围矩形苗圃![]() 的面积最大值;
的面积最大值;
(3)当所围矩形苗圃![]() 的面积为
的面积为![]() 时,则
时,则![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;
(2)当点P在射线BA上时,设![]() ,求y关于
,求y关于![]() 的函数解析式及定义域;
的函数解析式及定义域;
(3)联结PQ,直线PQ与直线BC交于点E,如果![]() 与
与![]() 相似,求线段BP的长.
相似,求线段BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
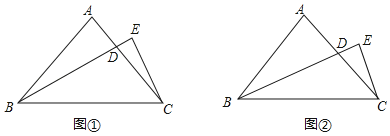
【题目】已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过点C作CE⊥BD,交BD的延长线于点E,如图①.
(1)求证:ADCD=BDDE;
(2)若BD是边AC的中线,如图②,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边长AB=2,BC=4,动点P从点B出发,沿B→C→D→A的路线运动,设△ABP的面积为S,点P走过的路程为x.
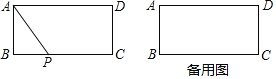
(1)当点P在CD边上运动时,△ABP的面积是否变化,请说明理由;
(2)求S与x之间的函数关系式;
(3)当S=2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
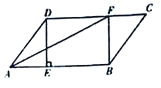
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com