
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G.
(1)求证:GC是⊙F的切线;
(2)填空:①若△BCF的面积为15,则△BDA的面积为 .
②当∠GCD的度数为 时,四边形EFCD是菱形.
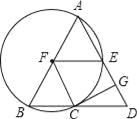
【答案】证明见解析(2)60(3)30°
【解析】试题分析:(1)由等腰三角形的性质得出∠D=∠BCF,证出CF∥AD,由已知条件得出CG⊥CF,即可得出结论;
(2)①根据平行线的性质得出△BCF∽△BDA,得出![]() ,△BCF的面积:△BDA的面积=1:4,即可得出结果;
,△BCF的面积:△BDA的面积=1:4,即可得出结果;
②证出△BCF是等边三角形,得出∠B=60°,CF=BF=![]() AB,证出△ABD是等边三角形,CF=
AB,证出△ABD是等边三角形,CF=![]() AD,证出△AEF是等边三角形,得出AE=AF=
AD,证出△AEF是等边三角形,得出AE=AF=![]() AB=
AB=![]() AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
试题解析:(1)∵AB=AD,FB=FC,
∴∠B=∠D,∠B=∠BCF,
∴∠D=∠BCF,
∴CF∥AD,
∵CG⊥AD,
∴CG⊥CF,
∴GC是⊙F的切线;
(2)解:①∵CF∥AD,
∴△BCF∽△BDA,
∴![]() =
=![]() ,△BCF的面积:△BDA的面积=1:4,
,△BCF的面积:△BDA的面积=1:4,
∴△BDA的面积=4△BCF的面积=4×15=60;
故答案为:60;
②当∠GCD的度数为30°时,四边形EFCD是菱形.理由如下:
∵CG⊥CF,∠GCD=30°,
∴∠FCB=60°,
∵FB=FC,
∴△BCF是等边三角形,
∴∠B=60°,CF=BF=![]() AB,
AB,
∵AB=AD,
∴△ABD是等边三角形,CF=![]() AD,
AD,
∴∠A=60°,
∵AF=EF,
∴△AEF是等边三角形,
∴AE=AF=![]() AB=
AB=![]() AD,
AD,
∴CF=DE,
又∵CF∥AD,
∴四边形EFCD是平行四边形,
∵CF=EF,
∴四边形EFCD是菱形;
故答案为:30°.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( ) 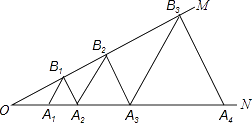
A.6
B.12
C.32
D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程(m﹣3)x2+2mx+m+1=0有两个不相等的实数根,并且这两个根又不互为相反数.
(1)求m的取值范围;
(2)当m在取值范围内取最小正偶数时,求方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面生活中的物体的运动情况可以看成平移的是( )
A.随风摆动的旗帜B.摆动的钟摆
C.汽车玻璃上的雨刷的运动D.从楼顶自由下落的球(球不旋转)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l是一次函数y=kx+b的图象,点A、B在直线l上.根据图象回答下列问题:
(1)写出方程kx+b=0的解;
(2)写出不等式kx+b>1的解集;
(3)若直线l上的点P(m,n)在线段AB上移动,则m、n应如何取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
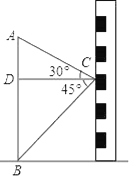
【题目】如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:![]() ≈1.73,
≈1.73,![]() ≈1.41,结果精确到0.1米)
≈1.41,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD中,BC∥AD,∠A=90°,点P从A点出发,沿折线AB→BC→CD运动,到点D时停止,已知△PAD的面积s与点P运动的路程x的函数图象如图②所示,则点P从开始到停止运动的总路程为( )
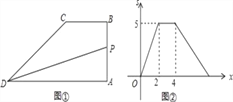
A. 4 B. 2+![]() C. 5 D. 4+
C. 5 D. 4+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com