
【题目】如图,反比例函数![]() (x>0)的图象与直线
(x>0)的图象与直线![]() 相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为_______________.
相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为_______________.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
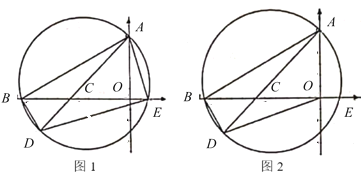
【题目】如图1,在平面直角坐标系中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,点
,点![]() 为
为![]() 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点![]() 、
、![]() 、
、![]() 作
作![]() 的外接圆
的外接圆![]() ,连结
,连结![]() 并延长交圆于点
并延长交圆于点![]() ,连结
,连结![]() 、
、![]() .
.
(1)求证:![]() .
.
(2)当![]() 时,求
时,求![]() 的长度.
的长度.
(3)如图2,连结![]() ,求线段
,求线段![]() 的最小值及当
的最小值及当![]() 最小时
最小时![]() 的外接圆圆心
的外接圆圆心![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有1500名学生,小明想了解全校学生每月课外阅读书籍的数量情况,随机抽取了部分学生,得到如统计图:
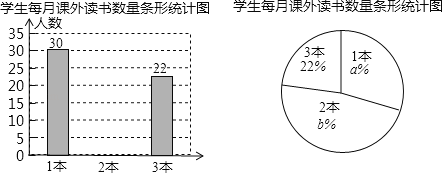
(1)一共抽查了多少人?
(2)每月课外阅读书籍数量是1本的学生对应的圆心角度数是多少?
(3)估计该校全体学生每月课外阅读书籍的总量大约是多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B为反比例函数y=![]() (k>0,x>0)上的两个动点,以A,B为顶点构造菱形ABCD.
(k>0,x>0)上的两个动点,以A,B为顶点构造菱形ABCD.
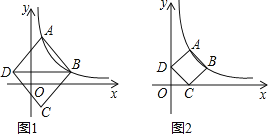
(1)如图1,点A,B横坐标分别为1,4,对角线BD∥x轴,菱形ABCD面积为![]() ,求k的值.
,求k的值.
(2)如图2,当点A,B运动至某一时刻,点C,点D恰好落在x轴和y轴正半轴上,此时∠ABC=90°,求点A,B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
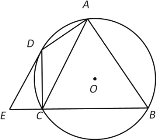
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=12,CE=3时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是

A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:
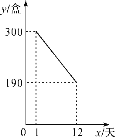
【题目】某公司开发出一款新包装的牛奶,牛奶的成本价为6元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/盒.前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前12天日销售量y(盒)与销售时间x(天)之间的函数关系,于是从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒.
(1)打折销售后,第17天的日销售量为________盒;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)已知日销售利润不低于560元的天数共有6天,设打折销售的折扣为a折,试确定a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣m)2+2(x﹣m)(m为常数)
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)当m取什么值时,该函数的图象关于y轴对称?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点三点![]() ,
,![]() ,
,![]() .
.
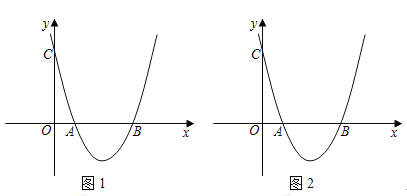
(1)求抛物线的解析式和对称轴;
(2)![]() 是抛物线对称轴上的一点,求满足
是抛物线对称轴上的一点,求满足![]() 的值为最小的点
的值为最小的点![]() 坐标(请在图1中探索);
坐标(请在图1中探索);
(3)在第四象限的抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是以
是以![]() 为对角线且面积为
为对角线且面积为![]() 的平行四边形?若存在,请求出点
的平行四边形?若存在,请求出点![]() 坐标,若不存在请说明理由.(请在图2中探索)
坐标,若不存在请说明理由.(请在图2中探索)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com