
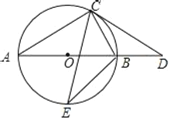
【题目】AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB的延长线相交于点D,CA=CD.
(1)连接BC,求证:BC=OB;
(2)E是![]() 中点,连接CE,BE,若BE=2,求CE的长.
中点,连接CE,BE,若BE=2,求CE的长.
【答案】(1)见解析;(2)1+![]() .
.
【解析】
(1)连接OC,根据圆周角定理、切线的性质得到∠ACO=∠DCB,根据CA=CD得到∠CAD=∠D,证明∠COB=∠CBO,根据等角对等边证明;
(2)连接AE,过点B作BF⊥CE于点F,根据勾股定理计算即可.
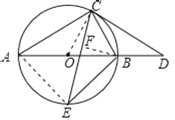
(1)证明:连接OC,
∵AB为⊙O直径,
∴∠ACB=90°,
∵CD为⊙O切线
∴∠OCD=90°,
∴∠ACO=∠DCB=90°﹣∠OCB,
∵CA=CD,
∴∠CAD=∠D.
∴∠COB=∠CBO.
∴OC=BC.
∴OB=BC;
(2)连接AE,过点B作BF⊥CE于点F,
∵E是AB中点,
∴![]() ,
,
∴AE=BE=2.
∵AB为⊙O直径,
∴∠AEB=90°.
∴∠ECB=∠BAE=45°,![]() ,
,
∴![]() .
.
∴CF=BF=1.
∴![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() .点
.点![]() 是
是![]() 的中点,在
的中点,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
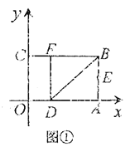
(Ⅰ)求点![]() 、
、![]() 的坐标;
的坐标;
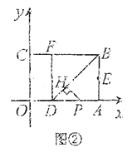
(Ⅱ)如图②,若点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 于
于![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的面积为
的面积为![]() ,试用关于
,试用关于![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅲ)在![]() 轴、
轴、![]() 轴上分别存在点
轴上分别存在点![]() 、
、![]() ,使得四边形
,使得四边形![]() 的周长最小,请直接写出四边形
的周长最小,请直接写出四边形![]() 的周长最小值.
的周长最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
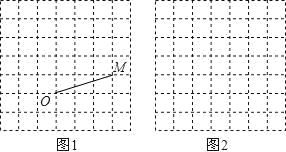
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;
(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
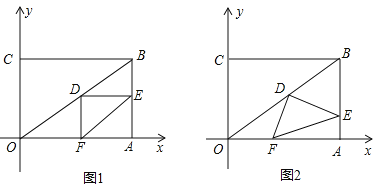
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的落实阳光体育运动,学校需要购买一批足球和篮球,已知一个足球比一个篮球的进价高30元,买一个足球和两个篮球一共需要300元.
(1)求足球和篮球的单价;
(2)学校决定购买足球和篮球共100个,为了加大校园足球活动开展力度,现要求购买的足球不少于60个,且用于购买这批足球和篮球的资金最多为11000元.试设计一个方案,使得用来购买的资金最少,并求出最小资金数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的体育达标情况,随机抽取![]() 名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
测试成绩(分) |
|
|
|
|
|
人数(人) |
|
|
|
|
|
(1)该校九年级有![]() 名学生,估计体育测试成绩为
名学生,估计体育测试成绩为![]() 分的学生人数;
分的学生人数;
(2)该校体育老师要对本次抽测成绩为![]() 分的甲、乙、丙、丁
分的甲、乙、丙、丁![]() 名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
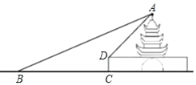
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足函数关系式
(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材每天的市场需求量
,从市场反馈的信息发现,该半成品食材每天的市场需求量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足一次函数关系,部分数据如表:
(元/千克)满足一次函数关系,部分数据如表:
销售价格 | 2 | 4 | …… | 10 |
市场需求量 | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格![]() 不低于2元/千克且不高于10元/千克.
不低于2元/千克且不高于10元/千克.
(1)直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种半成品食材能全部售出,而当每天的产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.
①当每天的半成品食材能全部售出时,求![]() 的取值范围;
的取值范围;
②求厂家每天获得的利润y(百元)与销售价格![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,当![]() 为______元/千克时,利润
为______元/千克时,利润![]() 有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则
有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则![]() 应定为______元/千克.
应定为______元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com