
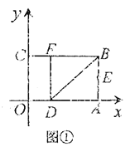
【题目】如图①,将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() .点
.点![]() 是
是![]() 的中点,在
的中点,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
(Ⅰ)求点![]() 、
、![]() 的坐标;
的坐标;
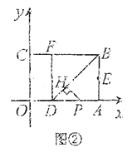
(Ⅱ)如图②,若点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 于
于![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的面积为
的面积为![]() ,试用关于
,试用关于![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅲ)在![]() 轴、
轴、![]() 轴上分别存在点
轴上分别存在点![]() 、
、![]() ,使得四边形
,使得四边形![]() 的周长最小,请直接写出四边形
的周长最小,请直接写出四边形![]() 的周长最小值.
的周长最小值.
【答案】(Ⅰ)E(3,1),F(1,2);(Ⅱ)S=![]() -
-![]() +
+![]() ;(Ⅲ)5+
;(Ⅲ)5+![]() ;
;
【解析】
(Ⅰ)求出CF和AE的长度即可写出点的坐标;
(Ⅱ)用x表示出PD长度,结合三角函数进一步表示DH,PH的长度,运用三角形面积公式即可求解;
(Ⅲ)作点F关于y轴的对称点F′,点E关于x轴的对称点E′,连接E′F′交y轴于点N,交x轴于点M,此时四边形MNFE的周长最小,根据轴对称的性质可得四边形MNFE的周长=E′F′+EF,根据两点间的距离公式即可得出结论.
(Ⅰ)∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
∴OA=3,AB=2
根据矩形OABC可得:AB=OC=2,BC=OA=3
由可翻折的性质可得:BF=AB=2,
∴CF=BC-BF=1,
∵点![]() 是
是![]() 的中点,∴AE=1,
的中点,∴AE=1,
∴E(3,1),F(1,2);
(Ⅱ)如图2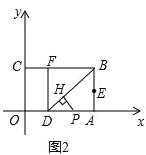
∵将△BDA沿BD翻折,使点A落在BC边上的点F处,
∴BF=AB=2,
∴OD=CF=3-2=1,
∵![]() =
=![]() ,OD=1,∴PD=x-1,
,OD=1,∴PD=x-1,
在Rt△ABD中,AB=2,AD=2,∴∠ADB=45°,
在Rt△PDH中,PH=DH=![]() DP=
DP=![]() (x-1),
(x-1),
∴S=![]() ×DH×PH=
×DH×PH=![]() ×
×![]() (x-1)×
(x-1)×![]() (x-1)=
(x-1)=![]() -
-![]() +
+![]() ;
;
(Ⅲ)如图3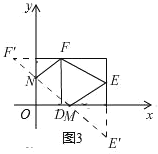
作点F关于y轴的对称点F′,点E关于x轴的对称点E′,连接E′F′交y轴于点N,交x轴于点M,此时四边形MNFE的周长最小,
∵点F(1,2)关于y轴的对称点F′(-1,2),
∵点E(3,1)关于x轴的对称点E′(3,-1),
∴F′N=FN, E′M=EM
∴四边形MNFE的周长=E′F′+EF=![]() ;
;
∴四边形MNFE周长的最小值为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点M处练习发球,将球从M点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足抛物线解析式.已知球达到最高2.6m的D点时,与M点的水平距离EM为6m.
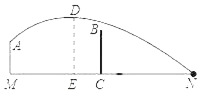
(1)在图中建立恰当的直角坐标系,并求出此时的抛物线解析式;
(2)球网BC与点M的水平距离为9m,高度为2.43m.球场的边界距M点的水平距离为18m.该球员判断此次发出的球能顺利过网并不会出界,你认为他的判断对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE的垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是___________.(写出所有正确结论的序号)
①AM平分∠CAB;
②AM2=ACAB;
③若AB=4,∠APE=30°,则![]() 的长为
的长为![]() ;
;
④若AC=3,BD=1,则有CM=DM=![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
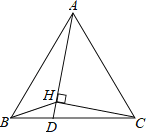
【题目】如图,△ABC是等边三角形,AB=![]() ,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元.
(1)求A,B两款毕业纪念册的销售单价;
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上,P为BC与网格线的交点,连接AP.

(Ⅰ)![]() 的长等于________;
的长等于________;
(Ⅱ)![]() 为边
为边![]() 上一点,请在如图所示的网格中,用无刻度的直尺,画出线段AQ,使
上一点,请在如图所示的网格中,用无刻度的直尺,画出线段AQ,使![]() ,并简要说明点Q的位置是如何找到的(不要求证明)_______.
,并简要说明点Q的位置是如何找到的(不要求证明)_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
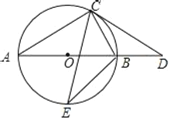
【题目】AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB的延长线相交于点D,CA=CD.
(1)连接BC,求证:BC=OB;
(2)E是![]() 中点,连接CE,BE,若BE=2,求CE的长.
中点,连接CE,BE,若BE=2,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com