
【题目】如图,排球运动员站在点M处练习发球,将球从M点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足抛物线解析式.已知球达到最高2.6m的D点时,与M点的水平距离EM为6m.
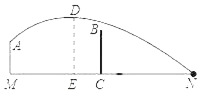
(1)在图中建立恰当的直角坐标系,并求出此时的抛物线解析式;
(2)球网BC与点M的水平距离为9m,高度为2.43m.球场的边界距M点的水平距离为18m.该球员判断此次发出的球能顺利过网并不会出界,你认为他的判断对吗?请说明理由.
【答案】(1)见解析,![]() ;(2)该球员的判断不对,球会出界,见解析.
;(2)该球员的判断不对,球会出界,见解析.
【解析】
(1)直角坐标系的建立要使点的坐标容易确定,因此可以以点M为坐标原点,建立平面直角坐标系,由题意即可确定点A,E,D的坐标,已知顶点D及抛物线上一点A的坐标,可设顶点式,利用待定系数法求解析式即可;(2)利用(1)所求解析式可求出球运行的高度和水平距离,与题中所给的球网BC的高度及球场的边界距M点的水平距离进行大小比较即可判断能否过网能否出界.
解:(1)如图,

以点M为坐标原点,建立平面直角坐标系,则点A,E,D的坐标分别为(0,2),(6,0),(6,2.6)
设球运行的高度y(m)与运行的水平距离x(m)的抛物线解析式为y=a(x﹣h)2+k
由题意知抛物线的顶点为(6,2.6)
故y=a(x﹣6)2+2.6
将点A(0,2)代入得2=36a+2.6
∴a=﹣![]() ,
,
故此时抛物线的解析式为y=﹣![]() (x﹣6)2+2.6
(x﹣6)2+2.6
(2)该球员的判断不对,理由如下:
当x=9时,y=﹣![]() (x﹣6)2+2.6=2.45>2.43
(x﹣6)2+2.6=2.45>2.43
∴球能过网;
当y=0时,﹣![]() (x﹣6)2+2.6=0
(x﹣6)2+2.6=0
解得:x1=6+![]() >18,x2=6﹣
>18,x2=6﹣![]() (舍)
(舍)
故球会出界.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一段抛物线![]() 为
为![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,顶点为
两点,顶点为![]() ;将
;将![]() 绕点
绕点![]() 旋转180°得到
旋转180°得到![]() ,顶点为
,顶点为![]() ;
;![]() 与
与![]() 组成一个新的图象.垂直于
组成一个新的图象.垂直于![]() 轴的直线
轴的直线![]() 与新图象交于点
与新图象交于点![]() ,
,![]() ,与线段
,与线段![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() ,
,![]() 均为正数,设
均为正数,设![]() ,则
,则![]() 的最大值是( )
的最大值是( )
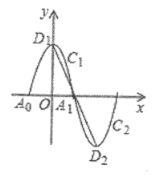
A. 15B. 18C. 21D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
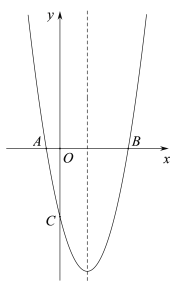
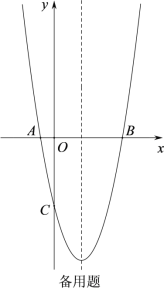
【题目】如图,抛物线![]() 的对称轴为直线x=2,抛物线与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0).
的对称轴为直线x=2,抛物线与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0).
(1)求抛物线的函数表达式;
(2)将抛物线![]() 图象x轴下方部分沿x轴向上翻折,保留抛物线在x轴上的点和x轴上方图象,得到的新图象与直线y=t恒有四个交点,从左到右四个交点依次记为D,E,F,G.当以EF为直径的圆过点Q(2,1)时,求t的值;
图象x轴下方部分沿x轴向上翻折,保留抛物线在x轴上的点和x轴上方图象,得到的新图象与直线y=t恒有四个交点,从左到右四个交点依次记为D,E,F,G.当以EF为直径的圆过点Q(2,1)时,求t的值;
(3)在抛物线![]() 上,当m≤x≤n时,y的取值范围是m≤y≤7,请直接写出x的取值范围.
上,当m≤x≤n时,y的取值范围是m≤y≤7,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”小长假期间,小李一家想到以下四个5A级风景区旅游:A.石林风景区;B.香格里拉普达措国家公园;C.腾冲火山地质公园;D.玉龙雪山景区.但因为时间短,小李一家只能选择其中两个景区游玩
(1)若小李从四个景区中随机抽出两个景区,请用树状图或列表法求出所有可能的结果;
(2)在随机抽出的两个景区中,求抽到玉龙雪山风景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() .点
.点![]() 是
是![]() 的中点,在
的中点,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
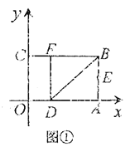
(Ⅰ)求点![]() 、
、![]() 的坐标;
的坐标;
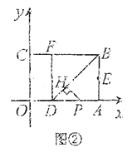
(Ⅱ)如图②,若点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 于
于![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的面积为
的面积为![]() ,试用关于
,试用关于![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅲ)在![]() 轴、
轴、![]() 轴上分别存在点
轴上分别存在点![]() 、
、![]() ,使得四边形
,使得四边形![]() 的周长最小,请直接写出四边形
的周长最小,请直接写出四边形![]() 的周长最小值.
的周长最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com