练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一段抛物线为，与轴交于，两点，顶点为；将绕点旋转180°得到，顶点为；与组成一个新的图象.垂直于轴的直线与新图象交于点，，与线段交于点，且，，均为正数，设，则的最大值是（ ）

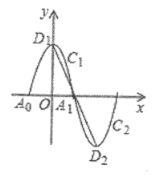
    A. 15B. 18C. 21D. 24

    【答案】B

    【解析】

    先求出绕点旋转180°得到的解析式，再根据，，均为正数且和最大，则可以得到l应在x轴的下方，根据二次函数的对称性可知x1+x2=12，由3≤x3≤6，推出x1+x2+x3的范围即可解决问题；

    解：翻折后的抛物线的解析式为y=（x-6）2-9=x2-12x+27，
    ∵设x1，x2，x3均为正数，
    ∴点P1（x1，y1），P2（x2，y2）在第四象限，
    根据对称性可知：x1+x2=12，
    ∵3≤x3≤6，
    ∴15≤x1+x2+x3≤18，即15≤t≤18，
    ∴的最大值是18

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某水果店5月份购进甲、乙两种水果共花费1700元，其中甲种水果8元/千克，乙种水果18元/千克.6月份，这两种水果的进价上调为：甲种水果10元/千克，乙种水果20元/千克.

    （1）若该店6月份购进这两种水果的数量与5月份都相同，将多支付货款300元，求该店5月份购进甲、乙两种水果分别是多少千克？

    （2）若6月份将这两种水果进货总量减少到120千克，且甲种水果不超过乙种水果的3倍，则6月份该店需要支付这两种水果的货款最少应是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】十八大以来，某校已举办五届校园艺术节.为了弘扬中华优秀传统文化，每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计，并绘制了如图所示不完整的折线统计图和扇形统计图.

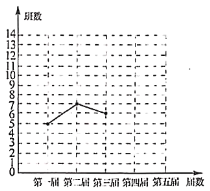
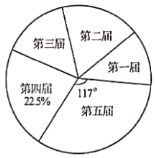
    (1)五届艺术节共有________个班级表演这些节日，班数的中位数为________，在扇形统计图中，第四届班级数的扇形圆心角的度数为________；

    (2)补全折线统计图；

    (3)第六届艺术节，某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用，，，表示).利用树状图或表格求出该班选择和两项的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知O为坐标原点，抛物线y1=ax2+bx+c（a≠0）与x轴相交于点A（x1，0），B（x2，0），与y轴交于点C，且O，C两点间的距离为3，x1x2＜0，|x1|+|x2|=4，点A，C在直线y2=-3x+t上．

    （1）求点C的坐标；

    （2）当y1随着x的增大而增大时，求自变量x的取值范围；

    （3）将抛物线y1向左平移n（n＞0）个单位，记平移后y随着x的增大而增大的部分为P，直线y2向下平移n个单位，当平移后的直线与P有公共点时，求2n2-5n的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线的顶点为A（1，4），抛物线与y轴交于点B（0，3），与x轴交于C，D两点．点P是x轴上的一个动点．

    （1）求此抛物线的解析式；

    （2）当PA+PB的值最小时，求点P的坐标；

    （3）抛物线上是否存在一点Q（Q与B不重合），使△CDQ的面积等于△BCD的面积？若存在，直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

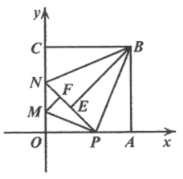
    【题目】如图，在平面直角坐标系第一象限中有正方形，，点是轴上一动点，将沿直线翻折后，点落在点处。在上有一点，使得将沿直线翻折后，点落在直线上的点处，直线交于点，连接.

    I.求证：；

    Ⅱ.求与的函数关系式，并求出的最大值；

    Ⅲ.当时，直接写出的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“世界读书日”前夕，某校开展了“读书助我成长”的阅读活动．为了了解该校学生在此次活动中课外阅读书籍的数量情况，随机抽取了部分学生进行调查，将收集到的数据进行整理，绘制出两幅不完整的统计图，请根据统计图信息解决下列问题：

    （1）求本次调查中共抽取的学生人数；

    （2）补全条形统计图；

    （3）在扇形统计图中，阅读本书籍的人数所在扇形的圆心角度数是　 　；

    （4）若该校有名学生，估计该校在这次活动中阅读书籍的数量不低于本的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，排球运动员站在点M处练习发球，将球从M点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足抛物线解析式．已知球达到最高2.6m的D点时，与M点的水平距离EM为6m．

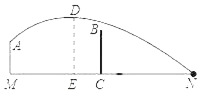
    （1）在图中建立恰当的直角坐标系，并求出此时的抛物线解析式；

    （2）球网BC与点M的水平距离为9m，高度为2.43m．球场的边界距M点的水平距离为18m．该球员判断此次发出的球能顺利过网并不会出界，你认为他的判断对吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，点P为AB延长线上的一点，过点P作⊙O的切线PE，切点为M，过A、B两点分别作PE的垂线AC、BD，垂足分别为C、D，连接AM，则下列结论正确的是___________.(写出所有正确结论的序号)

    ①AM平分∠CAB；

    ②AM2＝ACAB；

    ③若AB＝4，∠APE＝30°，则的长为；

    ④若AC＝3，BD＝1，则有CM＝DM＝.

    查看答案和解析>>

    同步练习册答案