
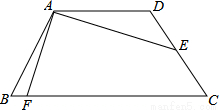
如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD= ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
A. B.
B. C.
C. D.
D.
D.
【解析】
试题分析:如答图,延长AE交BC的延长线于G,
∵E为CD中点,∴CE=DE.
∵AD∥BC,∴∠DAE=∠G=30°.
∵在△ADE和△GCE中,∠DAE=∠G,∠AED=∠GEC,CE=DE,
∴△ADE≌△GCE(AAS).∴CG=AD= ,AE=EG=2
,AE=EG=2 .∴AG=AE+EG=2
.∴AG=AE+EG=2 +2
+2 =4
=4 .
.
∵AE⊥AF,∴AF=AGtan30°= ,GF=AG÷cos30°=
,GF=AG÷cos30°= .
.
过点A作AM⊥BC于M,过点D作DN⊥BC于N,则MN=AD= ,
,
∵四边形ABCD为等腰梯形,∴BM=CN.
∵MG=AG•cos30°= ,∴CN=MG﹣MN﹣CG=6﹣
,∴CN=MG﹣MN﹣CG=6﹣ ﹣
﹣ =6﹣2
=6﹣2 .
.
∵AF⊥AE,AM⊥BC,∴∠FAM=∠G=30°.∴FM=AF•sin30°= .
.
∴BF=BM﹣MF=6﹣2 ﹣2=4﹣2
﹣2=4﹣2 .
.
故选D.

考点:1.等腰梯形的性质;2.平行的性质;3.全等三角形的判定和性质;4.锐角三角函数定义;5.特殊角的三角函数值.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源:2014-2015山东省威海市环翠区八年级上学期期中考试数学试卷(解析版) 题型:填空题
一组数据1,3,2,5,2,a的唯一众数是a,这组数据的中位数是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东卷)数学(解析版) 题型:解答题
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)。请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m)。(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:选择题
如果收入80元记作+80元,那么支出20元记作( )
A.+20元 B.﹣20元 C.+100元 D.﹣100元
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:解答题
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,
连接CD,已知∠CDB=∠OBD=30°.
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:填空题
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 ,则选取点B为坐标原点时的抛物线解析式是 .
,则选取点B为坐标原点时的抛物线解析式是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com