
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)。请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m)。(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:2014-2015山东省威海市环翠区七年级上学期期中考试数学试卷(解析版) 题型:解答题
如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,已知BE⊥AE,延长AE交BC的延长线于点F.

试说明:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东卷)数学(解析版) 题型:解答题
如图,在△ABC中,AB=AC,AD⊥AB点D,BC=10cm,AD=8cm,点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0)。

(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:解答题
关于体育选考项目统计图
项目 | 频数 | 频率 |
A | 80 | b |
B | c | 0.3 |
C | 20 | 0.1 |
D | 40 | 0.2 |
合计 | a | 1 |
(1)求出表中a,b,c的值,并将条形统计图补充完整.
表中a= ,b= ,c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球?

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:选择题
如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD= ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
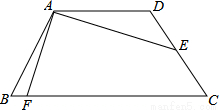
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:选择题
如图,正比例函数y=x与反比例函数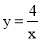 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于
的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于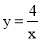 的函数值时,x的取值范围是( )
的函数值时,x的取值范围是( )

A.x>2 B.x<﹣2
C.﹣2<x<0或0<x<2 D.﹣2<x<0或x>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com