
在△ABC中,AB=6,BC=8,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1,若△CBC1的面积为16,求△ABA1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,直接写出线段EP1长度的最大值与最小值.

(1)60°;(2) ;(3)线段EP1长度的最大值为8,EP1长度的最小值1.
;(3)线段EP1长度的最大值为8,EP1长度的最小值1.
【解析】
试题分析:(1)由由旋转的性质可得:∠A1C1B=∠ACB=30°,BC=BC1,又由等腰三角形的性质,即可求得∠CC1A1的度数;
(2)由△ABC≌△A1BC1,易证得△ABA1∽△CBC1,然后利用相似三角形的面积比等于相似比的平方,即可求得△ABA1的面积;
(3)由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值.
(1)如图1,依题意得:△A1C1B≌△ACB.
∴BC1=BC,∠A1C1B=∠C=30°.
∴∠BC1C=∠C=30°.
∴∠CC1A1=60°;
(2)如图2,由(1)知:△A1C1B≌△ACB.
∴A1B=AB,BC1=BC,∠A1BC1=∠ABC.
∴∠ABA1=∠CBC1,
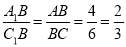
∴△A1BA∽△C1BC
∴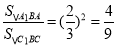
∵S△C1BC=3,
∴S△A1BA= ;
;
(3)线段EP1长度的最大值为8,EP1长度的最小值1.
解题过程如下:①如图a,过点B作BD⊥AC,D为垂足,
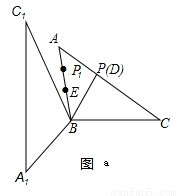
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin30°=6×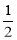 =3,
=3,
当P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1-BE=BD-BE=3-2=1;
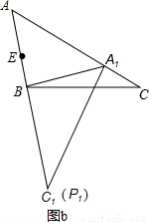
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=6+2=8.
综上所述,线段EP1长度的最大值为8,EP1长度的最小值1.
考点:相似形综合题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:2013-2014学年江苏省句容市九年级下学期期中考试(即一模)数学试卷(解析版) 题型:解答题
如图1所示,将一个边长为2的正方形 和一个长为2、宽为1的长方形
和一个长为2、宽为1的长方形 拼在一起,构成一个大的长方形
拼在一起,构成一个大的长方形 .现将小长方形
.现将小长方形 绕点
绕点 顺时针旋转至
顺时针旋转至 ,旋转角为
,旋转角为 .
.
(1)当点 恰好落在
恰好落在 边上时,求旋转角
边上时,求旋转角 的值;
的值;
(2)如图2, 为
为 的中点,且0°<
的中点,且0°< <90°,求证:
<90°,求证: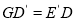 ;
;
(3)先将小长方形 绕点
绕点 顺时针旋转,使
顺时针旋转,使 与
与 全等(0°<
全等(0°< <180°),再将此时的小长方形
<180°),再将此时的小长方形 沿CD边竖直向上平移t个单位,设移动后小长方形边直线
沿CD边竖直向上平移t个单位,设移动后小长方形边直线 与BC交于点H,若DH∥FC,求上述运动变换过程中
与BC交于点H,若DH∥FC,求上述运动变换过程中 和t的值.
和t的值.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省句容市九年级下学期期中考试(即一模)数学试卷(解析版) 题型:填空题
若把代数式x2+2bx+4化为(x-m)2+k的形式,其中m、k为常数,则k-m的最大值是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市溧水区中考一模数学试卷(解析版) 题型:解答题
南京市体育中考现场考试男生有三项内容:三 分钟跳绳、1000米跑(二选一);引体向上、实心球(二选一);立定跳远、50米跑(二选一).小明三分钟跳绳是强项,他决定必选,其它项目在平时测试中成绩完全相同,他决定随机选择.
(1)用画树状图或列表的方法求:
①他选择的项目是三分钟跳绳、实心球、立定跳远的概率是 多少?
②他选择的项目中有立定跳远的概率是多少?
(友情提醒:各个项目可用A、B、C、…等符号来代表可简化解答过程)
(2)如果他决定用掷硬币的方法确定除三分钟跳绳外的其它两项考试项目,请你帮他设计一个合理的方案.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市溧水区中考一模数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,已知点A(2,0),⊙A的半径是2,⊙P的半径是1,满足与⊙A及y轴都相切的⊙P有 个.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:解答题
如图,以O为圆心的弧 度数为60 o,∠BOE=45o ,DA⊥OB,EB⊥OB.
度数为60 o,∠BOE=45o ,DA⊥OB,EB⊥OB.
(1)求 的值;
的值;
(2)若OE与 交于点M,OC平分∠BOE,连接CM.说明:CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.说明:CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com