
(12分)探究:
在矩形ABCD中,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.

(1)如图1,求证:ME=MF;
(2)如图2,点G是线段BC上一点,连接GE、GF、GM,若△EGF是等腰直角三角形,∠EGF=90°,求AB:AD的值;
(3)如图3,点G是线段BC延长线上一点,连接GE、GF、GM,若△EGF是等边三角形,直接写出AB、AD满足的数量关系.
见解析
【解析】
试题分析:(1)根据ABCD是矩形,得出∠EAM=∠FDM=90°,根据AM=DM,∠AME=∠FMD证出△AEM≌△DFM,即可得出ME=FM;(2)过点G作GH⊥AD于H,根据条件证出△AEM≌△HMG,得出GH=AM,因为点M是中点,所以AB=HG=AM=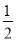 AD,所以AB:AD=2:1;(3)过点G作GH⊥AD交AD延长线于点H,连接MG,则∠GHM=∠A,根据△GEF是等边三角形,得出EM=FM,GM⊥EF,∠AME+∠GMH=90°,根据∠AME+∠AEM=90°,得出∠GMH=∠AEM,证出△AEM∽△HMG,所以
AD,所以AB:AD=2:1;(3)过点G作GH⊥AD交AD延长线于点H,连接MG,则∠GHM=∠A,根据△GEF是等边三角形,得出EM=FM,GM⊥EF,∠AME+∠GMH=90°,根据∠AME+∠AEM=90°,得出∠GMH=∠AEM,证出△AEM∽△HMG,所以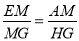 ,又根据题意可知∠MGF=∠EGM=30°,所以
,又根据题意可知∠MGF=∠EGM=30°,所以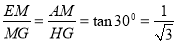 ,所以
,所以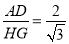 ,AB=HG,所以AB=
,AB=HG,所以AB=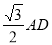 .
.
试题解析:(1)证明:在矩形ABCD中,∠A=∠FDM=90°.又∵AM=DM,∠AME=∠DMF,
∴△AME≌△DMF,∴ME=MF.
(2)【解析】
如图,过点G作GH⊥AD于点H.
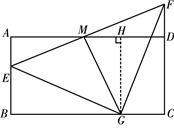
∴四边形ABGH是矩形.∵△EGF是等腰直角三角形,由(1)得,ME=MF,∴ME=MG,∠EMG=90°.
∴∠AME+∠DMG=∠HGM+∠DMG=90°,∴∠AME=∠HGM.又∵∠A=∠MHG,∴△AME≌△HGM
∴AM=HG.∴AB=HG=AM=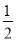 AD∴AD=2AB∴AB:AD=2:1
AD∴AD=2AB∴AB:AD=2:1
(3)AB=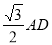
考点:1.矩形的性质;2.三角形的全等与相似;3.等腰三角形的性质;4.等边三角形的性质.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源:2013-2014学年黑龙江省绥棱县九年级(五四制)上学期期末考试数学试卷(解析版) 题型:解答题
(本题10分)某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元.若2元的奖品购买a件.
(1)用含a的代数式分别表示另外两种奖品的件数.
(2)请你设计购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省绥棱县九年级(五四制)上学期期末考试数学试卷(解析版) 题型:填空题
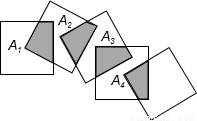
如图,把n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,……,An 分别是正方形的中心,n个这样的正方形重叠部分的面积和为 cm2.
得分 | 评卷人 |
|
|
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省绥棱县九年级(五四制)上学期期末考试数学试卷(解析版) 题型:填空题
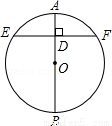
如图AB是⊙O的直径,弦EF⊥AB于点D,如果EF=10,AD=1,则⊙O半径的长是_ __.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省大石桥市中考模拟考试数学试卷(解析版) 题型:解答题
(10分)如图,△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC外角平分线,BE⊥AE,连接DE。

(1)求证:DA⊥AE;
(2)求证:四边形DCAE是平行四边形.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省南平市中考模拟数学试卷(解析版) 题型:解答题
一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同。
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于 ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市九年级下学期期中考试数学试卷(解析版) 题型:选择题
如图,坡角为 的斜坡上两树间的水平距离
的斜坡上两树间的水平距离 为
为 ,则两树间的坡面距离
,则两树间的坡面距离 为( )
为( )

A. B.
B. C.
C. D.
D.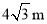
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com