
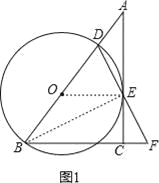
【题目】在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O.与AC相切于点E,连结DE并延长与BC的延长线交于点F.

(1)求证:EF2=BDCF;
(2)若CF=1,BD=5.求sinA的值.
【答案】(1)见解析;
(2)sinA=![]()
【解析】
试题(1)连接OE,由AC为圆O的切线,利用切线的性质得到OE垂直于AC,再由BC垂直于AC,得到OE与BC平行,根据O为DB的中点,得到E为DF的中点,即OE为三角形DBF的中位线,利用中位线定理得到OE为BF的一半,再由OE为DB的一半,求出BD=BF,证△BHE与△ECF相似即可;
(2)连接DQ,求出EF,根据勾股定理求出BE,根据三角形面积公式求出DQ,根据勾股定理求出BQ,求出∠BAC=∠BDQ,解直角三角形求出即可.
试题解析:(1)如图1,连接OE、BE,
∵AC与圆O相切,
∴OE⊥AC,
∵BC⊥AC,
∴OE∥BC,
又∵O为DB的中点,
∴E为DF的中点,即OE为△DBF的中位线,
∴OE=![]() BF,
BF,
又∵OE=![]() BD,
BD,
则BF=BD,
∵BD为⊙O直径,
∴∠BED=90°,
∵∠ACB=90°,
∴∠BEF=∠ECF=90°,
∵∠F=∠F,
∴△ECF∽△BEF,
∴![]() ,
,
∴EF2=BFCF=BDCF;
(2) 如图2,连接DQ,
∵EF2=BDCF,CF=1,BD=5,
∴EF=![]() ,
,
∵BD为⊙O的直径,
∴DQ⊥BF,BE⊥DF,
∵BD=BF,BD=5,
∴BF=5,DE=EF=![]() ,
,
即DF=2![]() ,
,
由勾股定理得:BE=![]() =2
=2![]() ,
,
∵在△BDF中,由三角形面积公式得:BF×DQ=DF×BE,
∴5DQ=2![]() ×2
×2![]() ,
,
∴DQ=4,
在Rt△BDQ中,BD=5,DQ=4,由勾股定理得:BQ=3,
∵∠ACB=90°,DQ⊥BF,
∴DQ∥AC,
∴∠A=∠BDQ,
∴sinA=sin∠BDQ=![]() .
.



科目:初中数学 来源: 题型:
【题目】定义:若抛物线![]() 上有两点
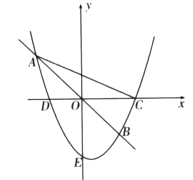
上有两点![]() 关于原点对称(点A在点B左侧)则称它为“完美抛物线”,如图.
关于原点对称(点A在点B左侧)则称它为“完美抛物线”,如图.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若抛物线![]() 是“完美抛物线”,求
是“完美抛物线”,求![]() 的值;
的值;
(3)若完美抛物线![]() 与
与![]() 轴交于点E与
轴交于点E与![]() 轴交于
轴交于![]() 两点(点D在点C的左侧),顶点为点
两点(点D在点C的左侧),顶点为点![]() ,
,![]() 是以
是以![]() 为直角边的直角三角形,点
为直角边的直角三角形,点![]() ,求点
,求点![]() 中
中![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
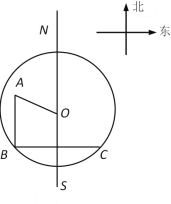
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.(本题参考数据:sin67.4°=![]() ,cos67.4°=
,cos67.4°=![]() ,tan67.4°=
,tan67.4°=![]() )
)
(1)求弦BC的长;
(2)请判断点A和圆的位置关系,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
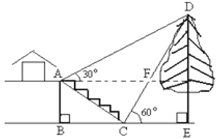
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=50°,则∠BDE= °.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com