
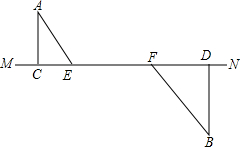
 如图,AC⊥MN于点C,BD⊥MN于点D,线段EF在线段CD上滑动.AC=3,BD=4,EF=5.设CE=x,CD=y.
如图,AC⊥MN于点C,BD⊥MN于点D,线段EF在线段CD上滑动.AC=3,BD=4,EF=5.设CE=x,CD=y.分析 (1)由全等三角形对应边相等可求得x、y的值;
(2)由相似三角形的性质可求得x、y之间的函数关系式;
(3)作BG∥MN,取BG=EF,连结AG交MN于点P,滑动EF使点E与点P重合,点F落到点Q处,此时AE+FB取最小值.根据平行四边形的性质可知AE+FB=AE+EG,由两点之间线段最短可知当点E与点P重合是AE+BF有最小值,然后由△ACP∽△BDQ列出比例式,从而可求得x的值.
解答 解:(1)∵△ACE≌△BDF,
∴FD=AC=3,CE=BD=4.
∴x=4,y=FD+EF+CE=3+5+4=12.
(2)∵△ACE∽△BDF,
∴$\frac{AC}{CE}=\frac{BD}{FD}$或$\frac{AC}{CE}=\frac{DF}{BD}$.
由$\frac{AC}{CE}=\frac{BD}{FD}$可知:$\frac{3}{x}=\frac{4}{y-x-5}$,整理得:y=$\frac{7}{3}x+5$;
由$\frac{AC}{CE}=\frac{DF}{BD}$可知.$\frac{3}{x}=\frac{y-x-5}{4}$,整理得;y=$\frac{12}{x}+x+5$.
∴y与x之间的函数关系式为:y=$\frac{7}{3}x+5$或y=$\frac{12}{x}+x+5$.
(3)作BG∥MN,取BG=EF,连结AG交MN于点P,滑动EF使点E与点P重合,点F落到点Q处,此时AE+FB取最小值.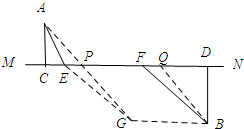
证明:连结BQ、GE.
∵BG∥EF,BG=EF,
∴四边形EGBF是平行四边形.
同理四边形PGBQ也是平行四边形.
∴EG=FB,PG=QB.
∴AE+BF=AE+EG.
∴当点E与点P重合时,AE+EG=AP+PG=AG.
由两点之间线段最短可知:AE+BF的最小值=AG.
∵PG∥QB,
∴∠GPQ=∠BQD.
∵∠APC=∠GPQ,
∴∠APC=∠BQD.
又∵∠ACP=∠BDQ,
∴△ACP∽△BDQ.
∴$\frac{AC}{CE}=\frac{BD}{DQ}$,即$\frac{3}{x}=\frac{4}{14-x-5}$.
解得:x=$\frac{27}{7}$.
点评 本题主要考查的是全等三角形的性质、相似三角形的性质和判定、平行四边形的性质和判定、线段的性质,明确当E与点P重合时AE+FB有最小值是解题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
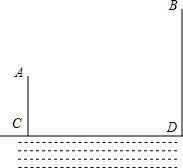 如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?
如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
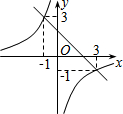 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )| A. | x<-1或0<x<3 | B. | -1<x<0或x>3 | C. | -1<x<0 | D. | x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
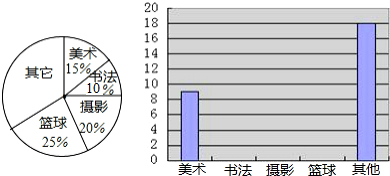
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
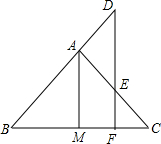 如图,在△ABC中,AB=AC,AM为△ABC底边上的中线,点D在BA的延长线上,E在AC上,且AD=AE,DE交BC于F,求证:DF⊥BC.
如图,在△ABC中,AB=AC,AM为△ABC底边上的中线,点D在BA的延长线上,E在AC上,且AD=AE,DE交BC于F,求证:DF⊥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com