
���� ��1����A�ͳ��ۼ�ΪxԪ��B�ͳ��ۼ�Ϊ��x-400��Ԫ������ͬ�������ij���B�ͳ��������ܶ���A�ͳ������ܶ��$\frac{4}{5}$���з�����⣻
��2����A�ͳ��ɹ�m����B�ͳ��ɹ���60-m��������������ɵã��ܽ�����7.8��Ԫ���ݴ��в���ʽ��⣻
��3����������=�ۼ�-���ۣ��г�����ʽ��������������жϣ�
��� �⣺��1����A�ͳ��ۼ�ΪxԪ��B�ͳ��ۼ�Ϊ��x-400��Ԫ��
������ã�$\frac{x-400}{x}$=$\frac{4}{5}$��
��ã�x=2000��
�����飬x=2000��ԭ��ʽ���̵Ľ⣬�ҷ������⣬
��x-400=1600��
��A�ͳ��ۼ�Ϊ2000Ԫ��B�ͳ��ۼ�Ϊ1600Ԫ��
��2����A�ͳ��ɹ�m����B�ͳ��ɹ���60-m������
������ã�1400m+1100��60-m����78000��
��ã�m��40��
��A�ͳ�����ܲɹ�40����
��3��������=��2000-1400��m+��1600-1100����60-m��
=100m+30000��
��������Ϊ3.5��ʱ��
100m+30000=35000��
��ã�m=50��
��A�ͳ��ɹ�50����B�ͳ��ɹ�10��ʱ������Ϊ3.5��
���� ���⿼���˷�ʽ���̵�Ӧ�ã������Ĺؼ��Ƕ������⣬���δ֪�����ҳ����ʵĵ�����ϵ���з�����⣬ע����飮


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У���OΪԲ�ģ��ʵ���Ϊ�뾶��������x���ڵ�M����y���ڵ�N���ٷֱ��Ե�M��NΪԲ�ģ�����MN�ij�Ϊ�뾶�����������ڵڶ������ڵ�P������P������Ϊ��2a��b+1������a��b��������ϵΪ��������
��ͼ����ƽ��ֱ������ϵ�У���OΪԲ�ģ��ʵ���Ϊ�뾶��������x���ڵ�M����y���ڵ�N���ٷֱ��Ե�M��NΪԲ�ģ�����MN�ij�Ϊ�뾶�����������ڵڶ������ڵ�P������P������Ϊ��2a��b+1������a��b��������ϵΪ��������| A�� | a-b | B�� | 2a+b=-1 | C�� | 2a-b=l | D�� | 2a+b=l |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
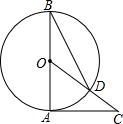 ��ͼ��AB�ǡ�O��ֱ����AC�ǡ�O�����ߣ�����OC����O�ڵ�D������BD������C=40�㣬���ODB�Ķ���Ϊ25�㣮
��ͼ��AB�ǡ�O��ֱ����AC�ǡ�O�����ߣ�����OC����O�ڵ�D������BD������C=40�㣬���ODB�Ķ���Ϊ25�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
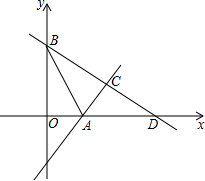 ��ͼ����ƽ��ֱ������ϵ�У���A��x����������ϣ���B��y����������ϣ����߶�OA��OB��OA��OB���ij��Ƿ���x2-9x+18=0����������
��ͼ����ƽ��ֱ������ϵ�У���A��x����������ϣ���B��y����������ϣ����߶�OA��OB��OA��OB���ij��Ƿ���x2-9x+18=0�����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 10�� | C�� | -2�� | D�� | -10�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com