
【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= . 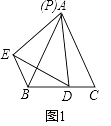
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?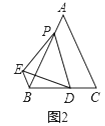
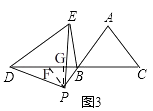
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)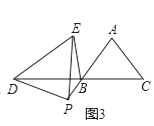
【答案】
(1)5
(2)解:如图2,过点P作PF∥AC交BC于F,
∴△FPB是等边三角形,
∴BF=PF=PB=AB﹣AP=4,∠BPF=60°,
∵△PDE是等边三角形,
∴PD=PE,∠DPE=60°,
∴∠BPE=∠FPD,
∴△PBE≌△PFD,
∴BE=DF,
∴BD+BE=BD+DF=BF=4;
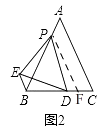
(3)解:如图3,
过点P作PF∥AC交BC于F,
∴∠BPF=∠BAC=70°,∠PFB=∠C,
∵AB=AC,∠BAC=70°,
∴∠ABC=∠C=55°,
∴∠PFB=∠C=∠PBF=55°,
∴PF=PB=a,
∵∠BPF=∠DPE=70°,
∴∠DPF=∠EPB,
∵PD=PE,
∴△PBE≌△PFD,
∴BE=DF,
过点P作PG⊥BC于G,
∴BF=2BG,
在Rt△BPG中,∠PBD=55°,
∴BG=BPcos∠PBD=acos55°,
∴BF=2BG=2acos55°,
∴BD﹣BE=BD﹣DF=BF=2acos55°.
【解析】解:(1)∵△ABC和△PDE是等边三角形,
∴PE=PD,AB=AC,∠DPE=∠CAB=60°,
∴∠BPE=∠CAD,
∴△PBE≌△ACD,
∴BE=CD,
∴BD+BE=BD+CD=BC=5,
所以答案是5;
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象的顶点坐标为(1, ![]() ),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
(1)求该二次函数的表达式;
(2)判断点B是否在此二次函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时生产同一种零件,在10天中两台机床每天生产的次品数如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
(1)分别计算两组数据的平均数和方差;
(2)从结果看,在10天中哪台机床出现次品的波动较小?
(3)由此推测哪台机床的性能较好
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).

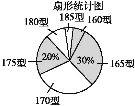
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解黔东南州某县2016届中考学生的体育考试得分情况,从该县参加体育考试的4 000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数直方图.
成绩分组 | 频数 |
25≤x<30 | 4 |
30≤x<35 | m |
35≤x<40 | 24 |
40≤x<45 | 36 |
45≤x<50 | n |
50≤x<55 | 4 |

(1)求m,n的值,并补全频数直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀的学生人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
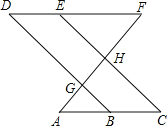
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若![]() ,
,![]() .
.
求证:![]() .
.
证明:![]()
![]() ______
______![]() 对顶角相等
对顶角相等![]()
![]() ,
,
![]() ______
______![]()
![]() ______
______![]() ______
______![]()
又![]()
![]() ,
,
![]() ______
______![]() ______
______![]()
![]() ______
______![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△ADE均为是顶角为42的等腰三角形,BC和DE分别是底边,图中△_________与△___________,可以通过以点________为旋转中心,旋转角度为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
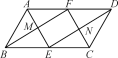
【题目】如图,ABCD中,∠ABC=60°,AB=4,AD=8,点E,F分别是边BC,AD的中点,点M是AE与BF的交点,点N是CF与DE的交点,则四边形ENFM的周长是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com