
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),下列说法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(
,且经过点(2,0),下列说法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(![]() ,y1)、(
,y1)、(![]() ,y2)是抛物线上的两点,则y1<y2;⑤
,y2)是抛物线上的两点,则y1<y2;⑤![]() >m(am+b)(其中m≠
>m(am+b)(其中m≠![]() ).其中说法正确的是_____
).其中说法正确的是_____
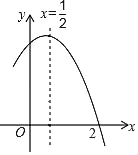
【答案】①②④⑤;
【解析】
①根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号②根据对称轴求出b=﹣a;③把x=2代入函数关系式,结合图象判断函数值与0的大小关系;④求出点(-![]() ,y1)关于直线x=
,y1)关于直线x=![]() 的对称点的坐标,根据对称轴即可判断y1和y2的大小,⑤根据最大值判断即可.
的对称点的坐标,根据对称轴即可判断y1和y2的大小,⑤根据最大值判断即可.
①∵图像开口向下,
∴a<0,
∵抛物线与y轴交于y轴正半轴,
∴c>0,
∵对称轴x= -![]() =
=![]() >0,
>0,
∴b>0,
∴abc<0,故①正确;
②将(2,0)代入y=ax2+bx+c (a≠0),
得4a+2b+c=0,
∵-![]() =
=![]() ,
,
∴a=﹣b,
∴﹣4b+2b+c=0,
∴﹣2b+c=0,故②正确;
③由②可知:4a+2b+c=0,故③错误;
④由于抛物线的对称轴为x=![]() ,
,
∴(![]() ,y1)与(
,y1)与(![]() ,y1)关于x=
,y1)关于x=![]() 对称,
对称,
∵由于x>![]() 时,y随着x的增大而减小,
时,y随着x的增大而减小,![]() >
>![]() ,
,
∴y1<y2 ,故④正确;
⑤由图象可知:x=![]() 时,y可取得最大值,且最大值为
时,y可取得最大值,且最大值为![]() a+
a+![]() b+c,
b+c,
∴m≠![]()
∴ a+ b+c>am2+bm+c,
∴![]() a+
a+![]() b>m(am+b),故⑤正确;
b>m(am+b),故⑤正确;
故答案为:①②④⑤;


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD 和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的是( )
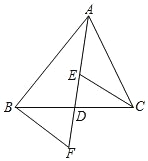
A. ①② B. ③⑤ C. ①③④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣bx+2(﹣2≤b≤2),当b从﹣2逐渐增加到2的过程中,它所对应的抛物线的位置也随之变动,下列关于抛物线的移动方向的描述中,正确的是( )
A. 先往左上方移动,再往左下方移动
B. 先往左下方移动,再往左上方移动
C. 先往右上方移动,再往右下方移动
D. 先往右下方移动,再往右上方移动
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()
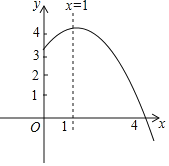
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;
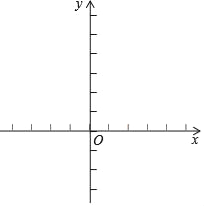
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
①abc<0;②2a﹣b<0;③a﹣b+c>0;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
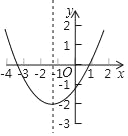
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+x+2
x2+x+2![]() 与x轴交于A,B两点,交y轴于点C,点C关于抛物线对称轴对称的点为D.
与x轴交于A,B两点,交y轴于点C,点C关于抛物线对称轴对称的点为D.
(1)求点D的坐标及直线AD的解析式;
(2)如图1,连接CD、AD、BD,点M为线段CD上一动点,过M作MN∥BD交线段AD于N点,点P是y轴上的动点,当△CMN的面积最大时,求△MPN的周长取得最小值时点P的坐标;
(3)如图2,线段AE在第一象限内交BD于点E,其中tan∠EAB=![]() ,将抛物线向右水平移动,点A平移后的对应点为点G;将△ABD绕点B逆时针旋转,旋转后的三角形纪为△A1BD1,若射线BD1与线段AE的交点为F,连接FG.若线段FG把△ABF分成△AFG和△BFG两个三角形,是否存在点G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
,将抛物线向右水平移动,点A平移后的对应点为点G;将△ABD绕点B逆时针旋转,旋转后的三角形纪为△A1BD1,若射线BD1与线段AE的交点为F,连接FG.若线段FG把△ABF分成△AFG和△BFG两个三角形,是否存在点G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=10,cosB=![]() ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
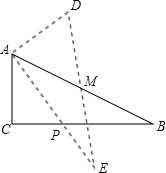
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com