
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
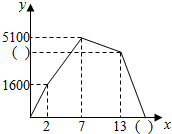 甲骑自行车,乙步行均从A地出发,以各自的速度匀速向B地行驶,其中甲先出发到达B地,停留6分钟后,按原路原速返回到A地,乙则一直步行到B地,如图是甲乙两人之间的距离y米与甲用时x之间的部分函数图象.
甲骑自行车,乙步行均从A地出发,以各自的速度匀速向B地行驶,其中甲先出发到达B地,停留6分钟后,按原路原速返回到A地,乙则一直步行到B地,如图是甲乙两人之间的距离y米与甲用时x之间的部分函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(1,0),(-3,0) |
| B、(1,0),(3,0) |
| C、(-1,0),(-3,0) |
| D、(3,0),(-1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、-|-3|>-2.4>-(-2)>+(-0.5 ) |
| B、-(-2)>-|-3|>-2.4>+(-0.5) |
| C、-(-2)>+(-0.5)>-2.4>-|-3| |
| D、-|-3|>-(-2)>-2.4>+(-0.5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com