
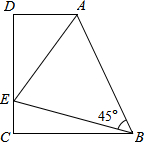
 如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.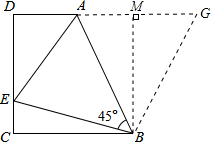 解:过B作DA的垂线交DA的延长线于M,M为垂足,
解:过B作DA的垂线交DA的延长线于M,M为垂足,
|
|


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
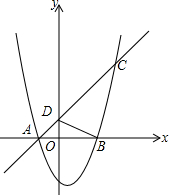 如图,一次函数y=x+m的图象经过点A(-2,0),交y轴于点D,对称轴为x=1的抛物线与x轴相交于点A、B,并与直线AD相交于点C,连接BD、BC,有∠OBD=∠BCD.
如图,一次函数y=x+m的图象经过点A(-2,0),交y轴于点D,对称轴为x=1的抛物线与x轴相交于点A、B,并与直线AD相交于点C,连接BD、BC,有∠OBD=∠BCD.查看答案和解析>>
科目:初中数学 来源: 题型:
 张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图(1),然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为10cm的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x,
张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图(1),然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为10cm的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x,查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、m=3,n=9 |
| B、m=9,n=9 |
| C、m=9,n=3 |
| D、m=3,n=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com