
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
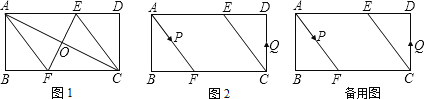
��1����ͼ1������AF��CE����֤�ı���AFCEΪ���Σ�����AF�ij���
��2����ͼ2������P��Q�ֱ��A��C����ͬʱ����������AFB����CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У�
����֪��P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬��A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
������P��Q���˶�·�̷ֱ�Ϊa��b����λ��cm��ab��0������֪A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���a��b�����������ϵʽ��
���𰸡���1��֤����������5cm��2����![]() ��a+b=12��ab��0��
��a+b=12��ab��0��
��������
�����������1����֤���ı���AFCEΪƽ���ı��Σ��ٸ��ݶԽ����ഹֱƽ�ֵ�ƽ���ı��������������ж������ݹ��ɶ����������AF�ij���
��2���ٷ�������ۿ�֪����P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴�ɣ�
�ڷ�����������ۿ�֪a��b�����������ϵʽ��
�⣺��1�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���CAD=��ACB����AEF=��CFE��
��EF��ֱƽ��AC������ΪO��
��OA=OC��
���AOE�ա�COF��
��OE=OF��
���ı���AFCEΪƽ���ı��Σ�
����EF��AC��
���ı���AFCEΪ���Σ�
�������εı߳�AF=CF=xcm����BF=��8��x��cm��
��Rt��ABF��AB=4cm��
�ɹ��ɶ�����42+��8��x��2=x2��
���x=5��
��AF=5cm��
��2������Ȼ��P����AF��ʱ��Q����CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
ͬ��P����AB��ʱ��Q����DE��CE�ϻ�P��BF��Q��CDʱ������ƽ���ı��Σ�Ҳ���ܹ���ƽ���ı��Σ�
���ֻ�е�P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��PC=QA��
����P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC=5t��QA=CD+AD��4t=12��4t����QA=12��4t��
��5t=12��4t��
���![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]() �룮
�룮
��������ã��ı���APCQ��ƽ���ı���ʱ����P��Q�ڻ���ƽ�еĶ�Ӧ���ϣ�
�����������
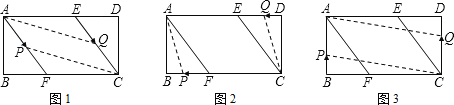
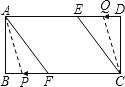
i����ͼ1����P����AF�ϡ�Q����CE��ʱ��AP=CQ����a=12��b����a+b=12��
ii����ͼ2����P����BF�ϡ�Q����DE��ʱ��AQ=CP����12��b=a����a+b=12��
iii����ͼ3����P����AB�ϡ�Q����CD��ʱ��AP=CQ����12��a=b����a+b=12��
����������a��b�����������ϵʽ��a+b=12��ab��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������һ�������߳�Ϊ 3 �� 5 �ĵ��������Σ���������������ε��ܳ�Ϊ�� ��
A. 11 B. 13 C. 8 D. 11��13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD��C��D���Ҳ࣬BEƽ����ABC��DEƽ����ADC��BE��DE����ֱ�߽��ڵ�E����ADC =70��.
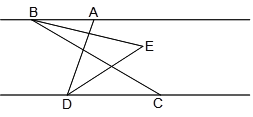
��1������EDC�Ķ�����
��2������ABC =n��������BED�Ķ������ú�n�Ĵ���ʽ��ʾ����
��3�����߶�BC��DC����ƽ�ƣ� ʹ�õ�B�ڵ�A���Ҳ࣬�����������䣬����ͼ�β��ж���BED�Ķ����Ƿ�ı䣬���ı䣬������Ķ������ú�n��ʽ�ӱ�ʾ�������ı䣬��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������н����ȷ���ǣ� ��
A.3a+2b=5ab
B.5y��3y=2
C.��3x+5x=��8x
D.3x2y��2x2y=x2y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���в���ȷ���ǣ� ��
A. �����ΰ��߷ֿɷ�Ϊ���ȱ������Ρ�����������
B. ���������ε��ڽǿ����Ƕ۽ǻ�ֱ��
C. ���������һ���Ƕ۽�
D. �����ε����߰������ηֳ������ȵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ݣ�0��1��2��3��3��5��5��10����λ���ǣ� ����
A. 2.5 B. 3 C. 3.5 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ƽ���ʽ������ǣ� ��
A. (2a+b)(2b-a) B. (3x-y)(-3x+y) C. (-m-n)(-m+n) D. (a+b)(-a-b)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�ڷ���������![]() ��ͼ���ϣ��ҵ�A��B�ĺ�����ֱ�Ϊa��2a��a��0����AC��x�ᣬ����ΪC������AOC�����Ϊ2��
��ͼ���ϣ��ҵ�A��B�ĺ�����ֱ�Ϊa��2a��a��0����AC��x�ᣬ����ΪC������AOC�����Ϊ2��
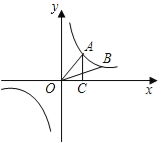
��1����÷����������Ľ���ʽ��
��2������AOB�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com