
|
|
|


科目:初中数学 来源: 题型:
 如图,直线AB与CD相交于点O,射线OF,OD分别是∠AOE,∠BOE的角平分线.
如图,直线AB与CD相交于点O,射线OF,OD分别是∠AOE,∠BOE的角平分线.| 1 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,O是坐标原点,抛物线y=ax2+bx与x轴正半轴交于点A,对称轴DE交x轴于点E.点B在第二象限,过点B作BC⊥x轴于点C,连结AB,且AB=10,AC=8.将点B向右平移5个单位后,恰好与抛物线的顶点D重合.
如图,在平面直角坐标系中,O是坐标原点,抛物线y=ax2+bx与x轴正半轴交于点A,对称轴DE交x轴于点E.点B在第二象限,过点B作BC⊥x轴于点C,连结AB,且AB=10,AC=8.将点B向右平移5个单位后,恰好与抛物线的顶点D重合.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
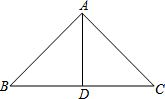 下面是小明同学在学了等腰三角形后所做的一道题,题目是这样的:“已知△ABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求∠BAC的度数.”
下面是小明同学在学了等腰三角形后所做的一道题,题目是这样的:“已知△ABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求∠BAC的度数.”| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,AB=AC,∠A=120°,BC=8cm,AB的垂直平分线交BC于点M,交AB于点D,AC的垂直平分线交BC于点N,交AC于点E,求MN的长.
如图,在△ABC中,AB=AC,∠A=120°,BC=8cm,AB的垂直平分线交BC于点M,交AB于点D,AC的垂直平分线交BC于点N,交AC于点E,求MN的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 某学习小组想了解南京市“迎青奥”健身活动的开展情况,准备采用以下调查方式中的一种进行调查:①从一个社区随机选取200名居民;②从一个城镇的不同住宅楼中随机选取200名居民;③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象.
某学习小组想了解南京市“迎青奥”健身活动的开展情况,准备采用以下调查方式中的一种进行调查:①从一个社区随机选取200名居民;②从一个城镇的不同住宅楼中随机选取200名居民;③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com