
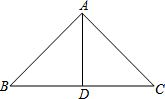
 下面是小明同学在学了等腰三角形后所做的一道题,题目是这样的:“已知△ABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求∠BAC的度数.”
下面是小明同学在学了等腰三角形后所做的一道题,题目是这样的:“已知△ABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求∠BAC的度数.”| 1 |
| 2 |
| 1 |
| 2 |
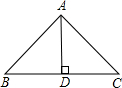
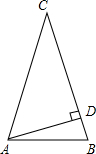 和
和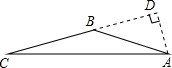 两种情况,
两种情况,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
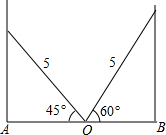 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.
如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、①和② | B、②和③ |
| C、③和④ | D、①和④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
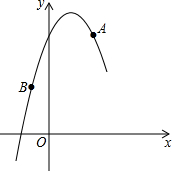 如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )
如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )| A、(-2,0) |
| B、(0.5,6.5) |
| C、(3,2) |
| D、(2,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com