
【题目】【问题情境】如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
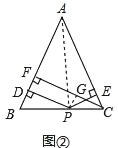
小丽给出的提示是:如图②,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
请根据小丽的提示进行证明.




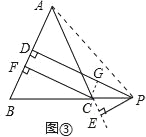
【变式探究】如图③,当点P在BC延长线上时,其余条件不变,试猜想PD、PE、CF三者之间的数量关系并证明.
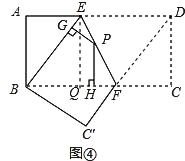
【结论运用】如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值.
【答案】见解析;CF=PD+PE ;PG+PH的值为4.
【解析】【问题情境】
分析:【问题情境】连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
【变式探究】连接AP,由△ABP与△ACP面积之差等于△ABC的面积可以证得:CF=PD-PE.
【结论运用】先证BE=BF,过点E作EQ⊥BF,垂足为Q,利用问题情境中的结论可得PG+PH=EQ,易证EQ=DC,故只需求出DC即可.
详解:证明:连接AP,如图②,
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP+S△ACP,
∴![]() ABCF=
ABCF=![]() ABPD+
ABPD+![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD+PE.
【变式探究】
证明:连接AP,如图③.
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP﹣S△ACP,
∴![]() ABCF=
ABCF=![]() ABPD﹣
ABPD﹣![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD﹣PE.
【结论运用】
过点E作EQ⊥BC,垂足为Q,如图④,
∵四边形ABCD是矩形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=8,CF=3,
∴BF=BC﹣CF=AD﹣CF=5.
由折叠可得:DF=BF,∠BEF=∠DEF.
∴DF=5.
∵∠C=90°,
∴DC=![]() =4.
=4.
∵EQ⊥BC,∠C=∠ADC=90°,
∴∠EQC=90°=∠C=∠ADC,
∴四边形EQCD是矩形,
∴EQ=DC=4.
∵AD∥BC,
∴∠DEF=∠EFB.
∵∠BEF=∠DEF,
∴∠BEF=∠EFB,
∴BE=BF.
由问题情境中的结论可得:PG+PH=EQ,
∴PG+PH=4,
∴PG+PH的值为4.


科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知线段a、b
(1)求作一个等腰△ABC,使底边长BC=a,底边上的高为b.(尺规作图,只保留作图痕迹)
(2)小明由此想到一个命题:等腰三角形底边的中点到两腰的距离相等,请你判断这个命题的真假,如果是真命题请证明;如果是假命题请举出反例.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程ax2+bx+c=0(a≠0)满足4a-2b+c=0,且有两个相等的实数根,则( )
A. b=aB. c=2aC. a(x+2)2=0(a≠0)D. a(x-2)2=0(a≠0)
查看答案和解析>>
科目:初中数学 来源: 题型:
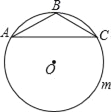
【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2![]() ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
A. y=![]() x+4 B. y=
x+4 B. y=![]() x+4 C. y=
x+4 C. y=![]() x2+4 D. y=
x2+4 D. y=![]() x2+4
x2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
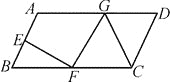
【题目】如图,在平行四边形ABCD中,E,F分别为AB,BC的中点,G是AD 上的任一点.计S1=S△BEF , S2=S△GFC ,S=S□ABCD ,则S=________S2=________S1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为参加学校运动会,七年级一班和七年级二班准备购买运动服. 下面是某服装厂给出的运动服价格表:
购买服装数(套) | 1~35 | 36~60 | 61及61以上 |
每套服装价(元) | 60 | 50 | 40 |
已知两班共有学生67人(每班学生人数都不超过60人),如果两班单独购买服装,每人只买一套,那么一共应付3650元. 问七年级一班和七年级二班各有学生多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
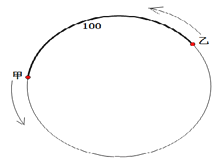
【题目】已知甲沿周长为300米的环形跑道上按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为t秒.
(1)若a=5,求甲、乙两人第1次相遇的时间;
(2)当t=50时,甲、乙两人第1次相遇.
①求a的值;
②若![]() 时,甲、乙两人第1次相遇前,当两人相距120米时,求
时,甲、乙两人第1次相遇前,当两人相距120米时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com