
【题目】已知函数 (
(![]() 为常数)
为常数)
(1)当![]() ,
,
①点![]() 在此函数图象上,求
在此函数图象上,求![]() 的值;
的值;
②求此函数的最大值.
(2)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,当此函数的图象与线段
,当此函数的图象与线段![]() 只有一个交点时,直接写出
只有一个交点时,直接写出![]() 的取值范围.
的取值范围.
(3)当此函数图象上有4个点到![]() 轴的距离等于4,求
轴的距离等于4,求![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ②
②![]() ;(2)
;(2)![]() ,
,![]() 时,图象与线段
时,图象与线段![]() 只有一个交点;(3)函数图象上有4个点到
只有一个交点;(3)函数图象上有4个点到![]() 轴的距离等于4时,
轴的距离等于4时,![]() 或
或![]() .
.
【解析】
(1)①将![]() 代入
代入![]() ;②当
;②当![]() 时,当
时,当![]() 时有最大值为5;当
时有最大值为5;当![]() 时,当
时,当![]() 时有最大值为
时有最大值为![]() ;故函数的最大值为
;故函数的最大值为![]() ;
;
(2)将点![]() 代入
代入![]() 中,得到
中,得到![]() ,所以
,所以![]() 时,图象与线段
时,图象与线段![]() 只有一个交点;将点
只有一个交点;将点![]() )代入
)代入![]() 和
和![]() 中,得到
中,得到![]() ,
,
所以![]() 时图象与线段
时图象与线段![]() 只有一个交点;
只有一个交点;
(3)当![]() 时,
时,![]() ,得到
,得到![]() ;当
;当![]() 时,
时,![]() ,得到
,得到![]() ,当
,当![]() 时,
时,![]() ,
,![]() .
.
解:(1)当![]() 时,
时,
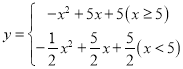 ,
,
①将![]() 代入
代入![]() ,
,
∴![]() ;
;
②当![]() 时,当
时,当![]() 时有最大值为5;
时有最大值为5;
当![]() 时,当
时,当![]() 时有最大值为
时有最大值为![]() ;
;
∴函数的最大值为![]() ;
;
(2)将点![]() 代入
代入![]() 中,
中,
∴![]() ,
,
∴![]() 时,图象与线段
时,图象与线段![]() 只有一个交点;
只有一个交点;
将点![]() 代入
代入![]() 中,
中,
∴![]() ,
,
将点![]() 代入
代入![]() 中,
中,
∴![]() ,
,
∴![]() 时图象与线段
时图象与线段![]() 只有一个交点;
只有一个交点;
综上所述:![]() ,
,![]() 时,图象与线段
时,图象与线段![]() 只有一个交点;
只有一个交点;
(3)当![]() 时,
时,![]() ,
,
![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,
,
![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ;
;
∴函数图象上有4个点到![]() 轴的距离等于4时,
轴的距离等于4时,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为![]() 时,求OA的长;
时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
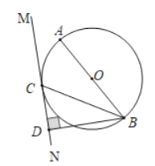
(1)求证:∠ABC=∠CBD;(2)若BC=4![]() ,CD=4,则⊙O的半径是 .
,CD=4,则⊙O的半径是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径CD垂直于弦AB,垂足为点E,∠ACD=22.5°,若CD=6cm,则AB的长为( )
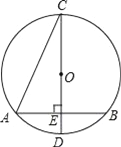
A. 4cm B. 3![]() cm C. 2
cm C. 2![]() cm D. 2
cm D. 2![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校对某班学生“五·一”小长假期间的度假情况进行调查,并根据收集的数据绘制了两幅不完整的统计图,请你根据图中提供的信息解答下面的问题:
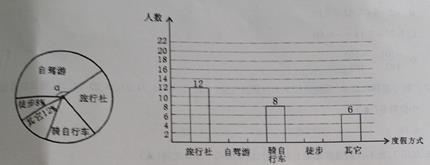
(1)求出该班学生的总人数.
(2)补全频数分布直方图.
(3)求出扇形统计图中∠α的度数.
(4)你更喜欢哪一种度假方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
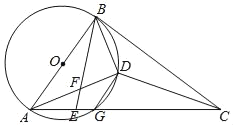
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
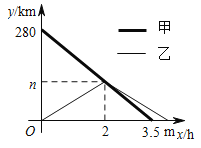
【题目】甲、乙两车分别从![]() 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到
两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到![]() 地,乙车立即以原速原路返回到
地,乙车立即以原速原路返回到![]() 地,甲、乙两车距
地,甲、乙两车距![]() 地的路程
地的路程![]() 与各自行驶的时间
与各自行驶的时间![]() 之间的关系如图所示.
之间的关系如图所示.
⑴![]() ________,
________,![]() ________;
________;
⑵求乙车距![]() 地的路程
地的路程![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
⑶当甲车到达![]() 地时,求乙车距
地时,求乙车距![]() 地的路程
地的路程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的点
的图象交于第二、四象限内的点![]() 和点
和点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,
,![]() 的面积为4.
的面积为4.
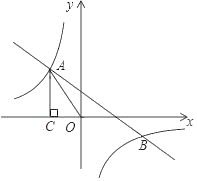
(1)分别求出![]() 和
和![]() 的值;
的值;
(2)结合图象直接写出![]() 的解集;
的解集;
(3)在![]() 轴上取点
轴上取点![]() ,使
,使![]() 取得最大值时,求出点
取得最大值时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com