
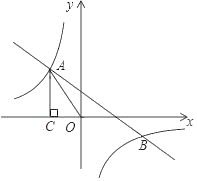
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的点
的图象交于第二、四象限内的点![]() 和点
和点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,
,![]() 的面积为4.
的面积为4.
(1)分别求出![]() 和
和![]() 的值;
的值;
(2)结合图象直接写出![]() 的解集;
的解集;
(3)在![]() 轴上取点
轴上取点![]() ,使
,使![]() 取得最大值时,求出点
取得最大值时,求出点![]() 的坐标.
的坐标.
科目:初中数学 来源: 题型:
【题目】已知函数 (
(![]() 为常数)
为常数)
(1)当![]() ,
,
①点![]() 在此函数图象上,求
在此函数图象上,求![]() 的值;
的值;
②求此函数的最大值.
(2)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,当此函数的图象与线段
,当此函数的图象与线段![]() 只有一个交点时,直接写出
只有一个交点时,直接写出![]() 的取值范围.
的取值范围.
(3)当此函数图象上有4个点到![]() 轴的距离等于4,求
轴的距离等于4,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是中华人民共和国建国70周年,襄阳市某学校开展了“我和我的祖国”主题学习竞赛活动.学校3000名学生全部参加了竞赛,结果所有学生成绩都不低于60分(满分100分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表.根据表中所给信息,解答下列问题:
成绩 | 频数 | 频率 |
| 15 | 0.30 |
|
| 0.40 |
| 10 |
|
| 5 | 0.10 |
(1)表中![]() ,
,![]() ;
;
(2)这组数据的中位数落在 范围内;
(3)判断:这组数据的众数一定落在![]() 范围内,这个说法 (填“正确”或“错误”);
范围内,这个说法 (填“正确”或“错误”);
(4)这组数据用扇形统计图表示,成绩在![]() 范围内的扇形圆心角的大小为 ;
范围内的扇形圆心角的大小为 ;
(5)若成绩不小于80分为优秀,则全校大约有 名学生获得优秀成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
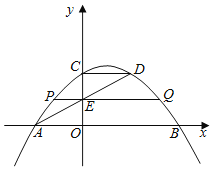
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在抛物线上,且
在抛物线上,且![]() .
.![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 的直线
的直线![]() 平行于
平行于![]() 轴,与拋物线相交于
轴,与拋物线相交于![]() 两点,则线段
两点,则线段![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)﹣(3)题
数学课上,老师出示了这样一道题:如图1,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() (其中
(其中![]() )
)![]() ,
,![]() 的平分线与
的平分线与![]() 相交于点
相交于点![]() ,
,![]() 垂足为
垂足为![]() ,探究线段
,探究线段![]() 与
与![]() 的数量关系,并证明.同学们经过思考后,交流了自已的想法:
的数量关系,并证明.同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段![]() 与
与![]() 的数量关系.”
的数量关系.”
……
老师:“保留原题条件,延长图1中的![]() ,与
,与![]() 相交于点
相交于点![]() (如图2),可以求出
(如图2),可以求出![]() 的值.”
的值.”
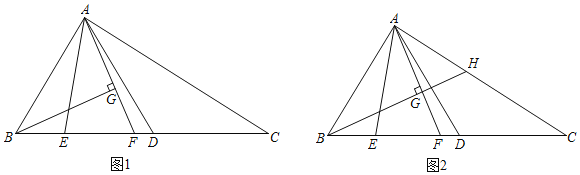
(1)求证:![]() ;
;
(2)探究线段![]() 与
与![]() 的数量关系(用含
的数量关系(用含![]() 的代数式表示),并证明;
的代数式表示),并证明;
(3)直接写出![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条公路旁依次有![]() 三个村庄,甲乙两人骑自行车分别从
三个村庄,甲乙两人骑自行车分别从![]() 村、
村、![]() 村同时出发前往
村同时出发前往![]() 村,甲乙之间的距离
村,甲乙之间的距离![]() 与骑行时间
与骑行时间![]() 之间的函数关系如图所示,下列结论:①
之间的函数关系如图所示,下列结论:①![]() 两村相距10
两村相距10![]() ;②出发1.25
;②出发1.25![]() 后两人相遇;③甲每小时比乙多骑行8
后两人相遇;③甲每小时比乙多骑行8![]() ;④相遇后,乙又骑行了15
;④相遇后,乙又骑行了15![]() 或65
或65![]() 时两人相距2
时两人相距2![]() .其中正确的个数是( )
.其中正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
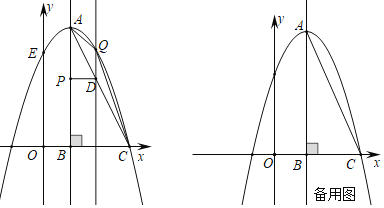
【题目】如图,在平面直角坐标系中,![]() 的边
的边![]() 在
在![]() 轴上,
轴上,![]() ,以
,以![]() 为顶点的抛物线
为顶点的抛物线![]() 经过点
经过点![]() ,交y轴于点
,交y轴于点![]() ,动点
,动点![]() 在对称轴上.
在对称轴上.
(1)求抛物线解析式;
(2)若点![]() 从
从![]() 点出发,沿
点出发,沿![]() 方向以1个单位/秒的速度匀速运动到点
方向以1个单位/秒的速度匀速运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 交抛物线于点
交抛物线于点![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 的面积最大?最大值是多少?
的面积最大?最大值是多少?
(3)若点![]() 是平面内的任意一点,在
是平面内的任意一点,在![]() 轴上方是否存在点
轴上方是否存在点![]() ,使得以点
,使得以点![]() 为顶点的四边形是菱形,若存在,请直接写出符合条件的
为顶点的四边形是菱形,若存在,请直接写出符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数;
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com