
分析 根据根与系数的关系得到α+β=$\frac{3}{2}$,αβ=-$\frac{1}{2}$,进一步把原式变形,然后利用整体思想计算即可.
(1)原式=(α+β)2-4αβ;(2)原式=$\frac{(α+β)^{2}-2αβ}{αβ}$;(3)原式=αβ-2(α+β)+4.
解答 解:∵α、β是一元二次方程2x2-3x-1=0的两个实数根,
∴α+β=$\frac{3}{2}$,αβ=-$\frac{1}{2}$,
(1)原式=(α+β)2-4αβ=$\frac{9}{4}$+2=$\frac{17}{4}$;
(2)原式=$\frac{(α+β)^{2}-2αβ}{αβ}$=$\frac{\frac{9}{4}+1}{-\frac{1}{2}}$=-$\frac{13}{2}$;
(3)原式=αβ-2(α+β)+4=-$\frac{1}{2}$-3+4=$\frac{1}{2}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程ax2+bx+c=0两个根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,渗透整体代入的思想.


科目:初中数学 来源: 题型:解答题
 如图,如果$\frac{AC}{AB}$=$\frac{CB}{AC}$,那么点C叫做线段AB的黄金分割点,$\frac{AC}{AB}$也就成为黄金分割比,你能算出这个比值吗?($\sqrt{5}$≈2.236)
如图,如果$\frac{AC}{AB}$=$\frac{CB}{AC}$,那么点C叫做线段AB的黄金分割点,$\frac{AC}{AB}$也就成为黄金分割比,你能算出这个比值吗?($\sqrt{5}$≈2.236)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
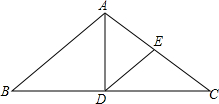 如图所示,已知:△ABC中,AB=AC,D是BC的中点,E是AC的中点,若∠EDC=∠C,BC=32cm,DE=10cm,求△ABC的面积.
如图所示,已知:△ABC中,AB=AC,D是BC的中点,E是AC的中点,若∠EDC=∠C,BC=32cm,DE=10cm,求△ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
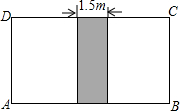 如图,一块长方形草地中间有一条小路,小路宽为1.5m,草地的长AB是宽AD的1.5倍,已知草地的面积(除小路外)为5310m2,求AB和AD的长.
如图,一块长方形草地中间有一条小路,小路宽为1.5m,草地的长AB是宽AD的1.5倍,已知草地的面积(除小路外)为5310m2,求AB和AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | △ABC是直角三角形,且∠C=90° | B. | △ABC是直角三角形,且∠A=90° | ||
| C. | △ABC是直角三角形,且∠B=90° | D. | △ABC不是直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com